なんで強化学習？

今回は強化学習の仕組みについてゆる〜くほざいていきたいと思います。

おい、なんでいきなり強化学習なんだよ。

はい！供養です。知識の。

斯々然々ありまして。。。

応答文作成というタスクに強化学習との組み合わせは使えるのか？

という疑問の元、強化学習を勉強したはいいが、

I have no idea ...

ということですが、せっかく勉強したので、 自分の為にアウトプットして、使える機会があれば取り出せるように、 今回は完全なる人類チラ裏計画です。

強化学習を単純に考えると 「報酬を与えることによって行動を促す」事だYO。

ゲームで例えるとスコアを取る、相手に勝つ、といった分かりやすい報酬があるのでイメージしやすいDESU。 つまり、これらの報酬を得られるようにコンピューターに計算させていくということになるでおじゃる。

強化学習の説明の続きをする前に、 よく誤解される「教師あり学習」と強化学習の違いを、軽く説明SURUZE。

「教師あり学習」は、 「行動する」と「行動した結果」の関連付け作業を 最初から教師（正解データ）が与えMASU。

一方、強化学習では、この関連付け作業を 学習を行っていく過程で、自分で「発見」をしていきMASU。

強化学習においてはさらに「罰則」が存在しMASU。

最終的に「玉」を取ることが「報酬」になりMASU。

逆に「玉」を取られることは「負ける」ことなので「罰則」になりMASU。

強化学習で出てくる専門用語「エージェント」を 「プレイヤー」とすると、

「エージェント」は「相手の玉を取る」ことを目的として、行動することにNARIMASU。

そして「玉を取られて負かされる」ことが罰則となり、これを避けるようにも行動するYO。

これをコンピューターによって「エージェント」は「何百回」も「実際に体験」することによって、こっちの選択肢が良かったなと「学習」するYO。

行動が単純に「報酬と罰則によって決定付けされている物事」なら コンピューターによってこの「訓練」を「短期間」で「繰り返す」ことによって 「エージェント」は「短時間」で賢くなり、「人が望む行動」してくれるようになるYO。

例えば「AlphaGo」などがそれにあたるYO。 近年では、チェスよりもAIが人に勝つことが難しいとされる「囲碁」で、 プロの囲碁棋士に対して、それもかなりの実績がある人物に対して、 勝ち越すなど、かなりの成果をあげているYO。

ゲームなどでは「高スコアをあげる」、「対戦で人に勝つ」ような行動が「報酬」にあたり、 「低スコア」「負ける」ような行動が罰則となり、 それを基に行動させるよう、コンピューターに計算させることができるYO。

じゃあ強化学習はこの「報酬」と「罰則」のルールをどのように決めてんの？

今からそのルールにあたる、アルゴリズム（計算方法）を、超超超簡略化して説明していきたいと思うYO。

それでは強化学習がどのように学習を進めていくかの概要を基本的なアルゴリズムQ-Learningで説明していきます。

状態と行動と報酬

ここで、簡単に３つの大事な要素を紹介します。

状態：s（State）：現在どのような状態、状況になっているかを示すもの。 将棋でいう「現在の譜面そのもの」や「戦況」など。

行動：a（Action）：どのような行動を起こすか。 将棋でいうなら「2六步を指す」や「7六歩を指す」など。

報酬：r（Reward）：行動を起こした結果の利益DESU。 将棋なら、最終局面においてかなり簡略化していますが、 下の図のような場面があるとすると、

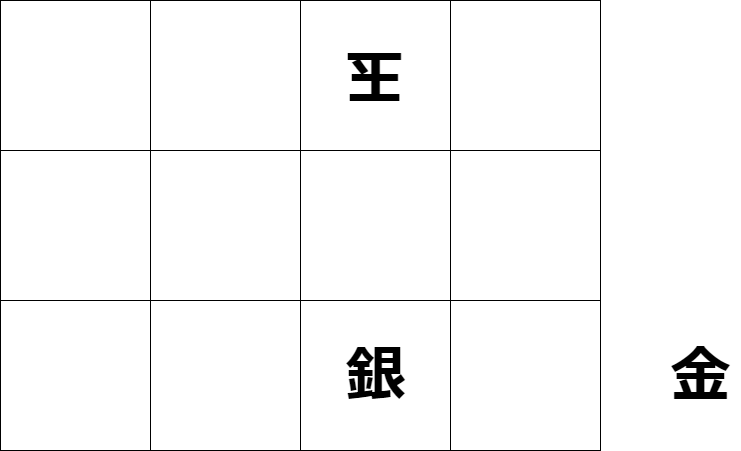
ここで、1二金と打つと、玉は3一玉と移動して、詰めなくなる。

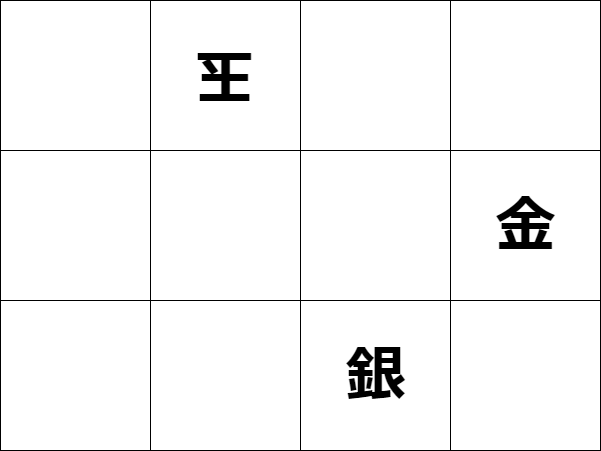
しかし、2二金と打てば、ここで詰みになる。

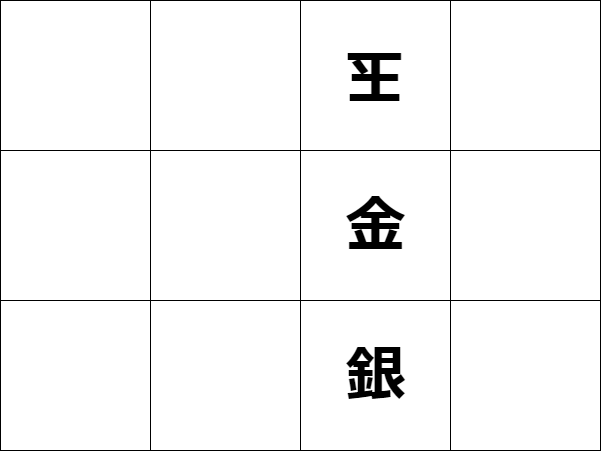
この詰みになることをReward（r：報酬）として、＋1点とすると 詰みにならない行動は（r：報酬）−１点。 その他を0点と決める。

将棋の場合持ち駒があるのでより複雑になるが、 ここでは簡略化して、持ち駒「金」を各マス目に置いた場合の点数を振り分ける。

ここで、あと何手か進めれば詰みになる可能性がある手に0点をつけているのは、 話をわかりやすくするため、あくまで「この１手で詰みになるものだけに」 報酬を与えているから。

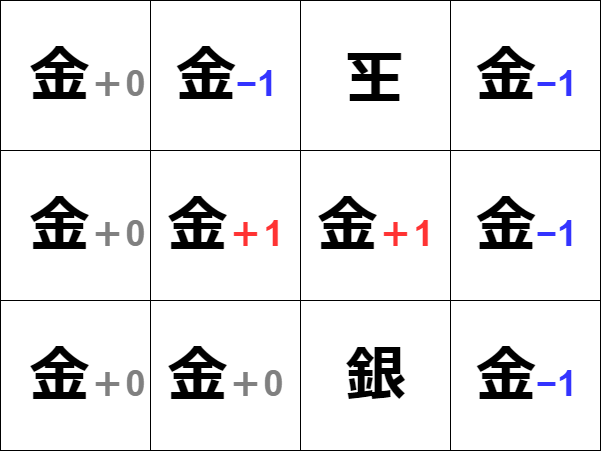
Q-Learningは極端にいうと、上の画像の左上（右上からでもいい） から順次「取り敢えず試してみて」、「その行動によってどんな報酬が得られたのか」 を計算していく方法になる。

状態行動価値Q：Q値=Q（ある時刻 s：状態 の時，ある a：行動 をとった時） この値を最大化していけばいい。

ここで上の画像を見て気付いたかたもいるかもしれませんが、 １手で詰む「2二金」と２手で詰む「3二金」が同じ＋１になっていMASU。

将棋の目的は「相手に勝つ」ことDESU。 どれだけ詰みに「手間」がかかったか、 美しい指し手を披露したら「点数が加算される」 といったことは加味されないYO。

（でもそんなアクロバティックな将棋あっても良いよNE！）

つまり、将来的に「相手を詰ませる」 「玉を奪う」＝「相手に勝てる」 1手であればどれだけ手間がかかろうが、 同じ1点とみなされる。

要するに短期的にもらえる報酬ではなく、 将来的にもらえる報酬を鑑みた値をみている。

しかし、実際問題としてはできるだけ最短で勝利を得たほうが その１手に「価値」があると考えるでSHO。

そこでγ（ガンマ）「時間割引率」の考えが出てくるYO。

この時間割引率に行動した回数を指数として累乗していき、 さらに報酬を掛けて加重していきMASU。

これにより、最終的には同じ報酬でも時間が経過するごとに最大値が減っていくように調整してあげる。

分かりやすく考えます。

ある状態：s：の時、ある行動：a：を取ると、将来的には同じ報酬：r：を受け取れるが 時間割引率：γ：を0．9と設定すると

時刻：t：の時の報酬を rt ＝R（st、at、s’t＋１）

rtが最終的に報酬＋１０を得られるとして、 行動回数を２回と４回に分けて時間割引された累積報酬を求めると

２回
行動回数＝２
9 ＝（0．9）^0＊rt（0） ＋（0．9）^1＊rt+1（10）

４回
行動回数＝４
7.29 ＝（0．9）^0＊rt（0） ＋（0．9）^1＊rt+1（0）＋（0．9）^2＊rt+2（0） ＋（0．9）^3＊rt+3（10）

となり、報酬が最大になるような方策（ポリシー）を見つけることが、強化学習の目的とすると

４回より、２回で報酬が最大となる方策（ポリシー）を選択するように学習していくよNE。

因みに、一回で目的が達成されれば当然の結果だけど、

10 ＝（0．9）^0＊rt（10）となるYO。

（将棋でたった１手で相手が「負けました」ってギャクだよね。）

あくまで単純化した計算モデルなので、 実際の数式やそれに至る考え方、その他の組み合わせて強化する理論を学びたいかたは 下記のWikipediaのページから参考文献のPDFを御覧KUDASAI。

Q-Learningをある方策のもと繰り返し、繰り返し行っていけば いつかは最適な値Q(s,a)を見つけてくれるYO。

QーLearningは単純なタスク。 決められた3×3ほどのマス目に チーズがあり、ネズミが歩いて チーズを食べるみたいな状況だと 直感的にも分かりやすく、 計算もすぐに終わるYO。

が、前述したみたいな「将棋」などは とても複雑な構成をしているYONE。

何せ、９マス×９マス棋盤に 駒数が自分相手合わせて、40。 駒ごとに動き方が違い、 二歩などの数種類の禁止ルールが存在し、 さらに相手の駒を再利用できる、持ち時間制限、 玉を囲う布陣、飛車角落ちハンデなど、 多種多様な戦略と戦術とそれに基づいた行動が存在するYONE。

ここで、Deep Learningの手法を組み合わせることができれば、最適な値Q(s,a)の近似値 を複雑な状況下に置いて導き出すことができることをGoogleの子会社ディープマインドが発見したYO！凄いね！
この方法の名前がそのままDeep Q-learningです。

DQNの説明の前に軽く、Deep Learningの芯の部分を説明します。

そうすればQ値の最適解を導く方法に何故Deep Learningの手法が使われたのかも理解でき、 さらに、今まで説明してきた簡単な強化学習の概念と実は似ていることにも気付くはず。

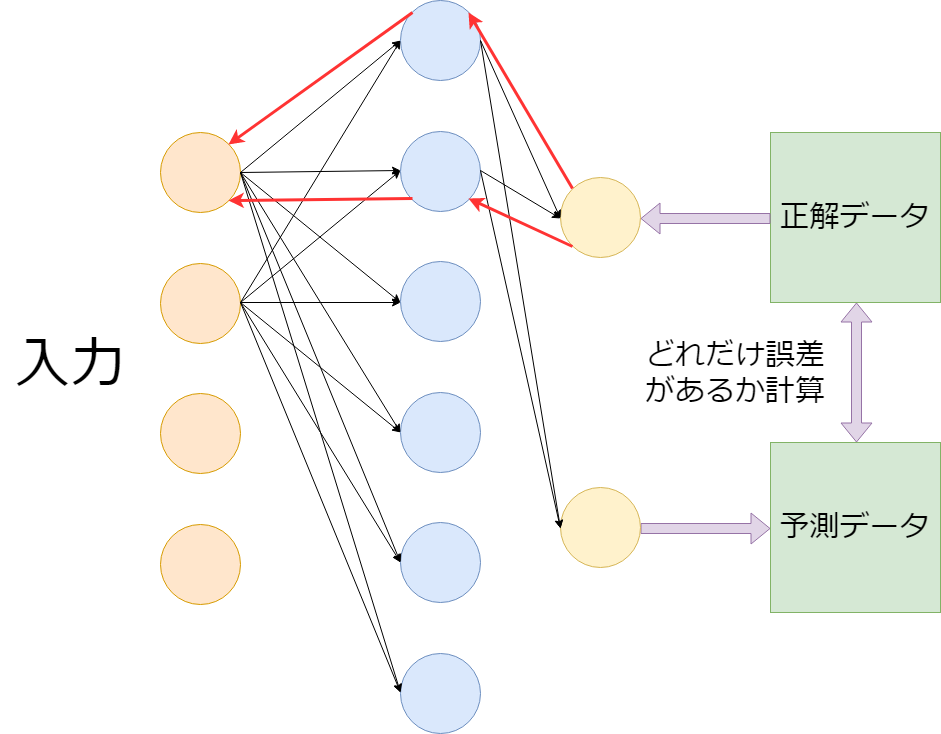
上の画像のニューラルネットワークから伸びる 矢印は省略してあります。

そして各矢印には「重み」と呼ばれる、 入力が出力に与える影響の「重要度」を調整する値が含まれているYO。

上の画像の赤い矢印こそDeep Learningの真髄です。

真髄ってなんかカッコイイ！ （これが北斗神拳の真髄だ！！）

簡略して説明するなら入力に対して出力した値を 正解データと見比べて、その誤差を計算。 そして、誤差伝搬法によって最適な重みを調整していき、 正解データに近付けることこそDeep LearningがやっているDAYO。

では、このDeep Learningモデルと、Q-learningを どのように組み合わせているのかを説明していきMASU。

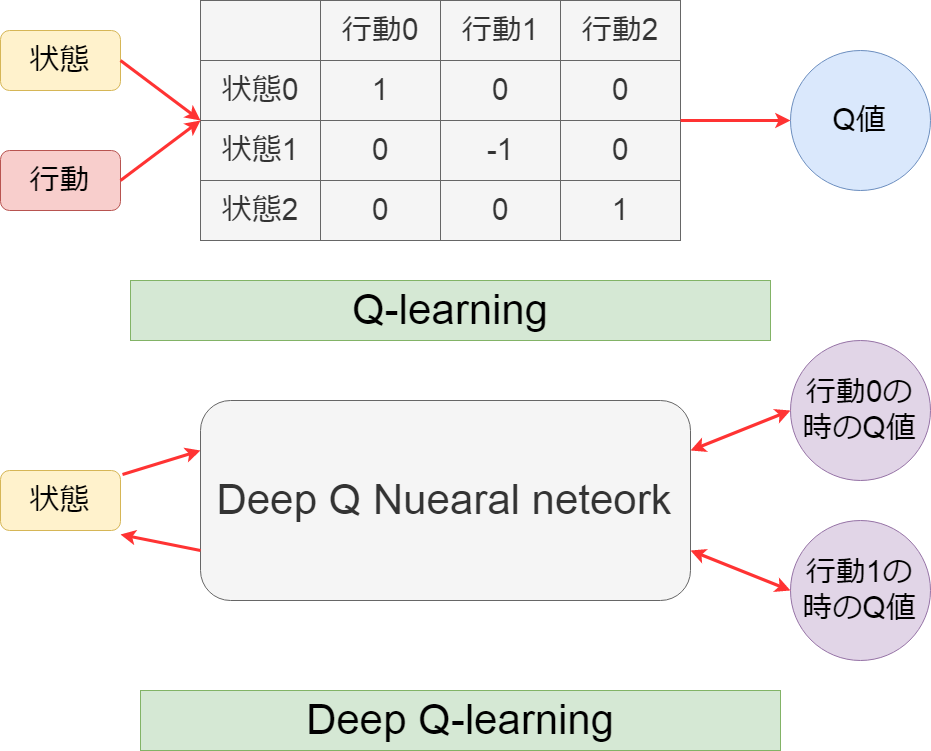
画像の上がQ-Learningを図解したもので、 下がDeep Q Learningを図解したものDESU。

Q-Learningは各時刻の行動：a：と状態：s：からQ-Tableを作り、それを基にQ値を導き出しMASU。

一方 Deep Q-Learningは各時刻の状態：s：が Q-Learning用のニューラルネットワーク層 を介して、各行動：a：の時のQ値を求めめ、 更にそれをまたQ-Learning用のニューラルネットワーク層に戻し、 逆伝播で重みを最適な値に更新していきMASU。

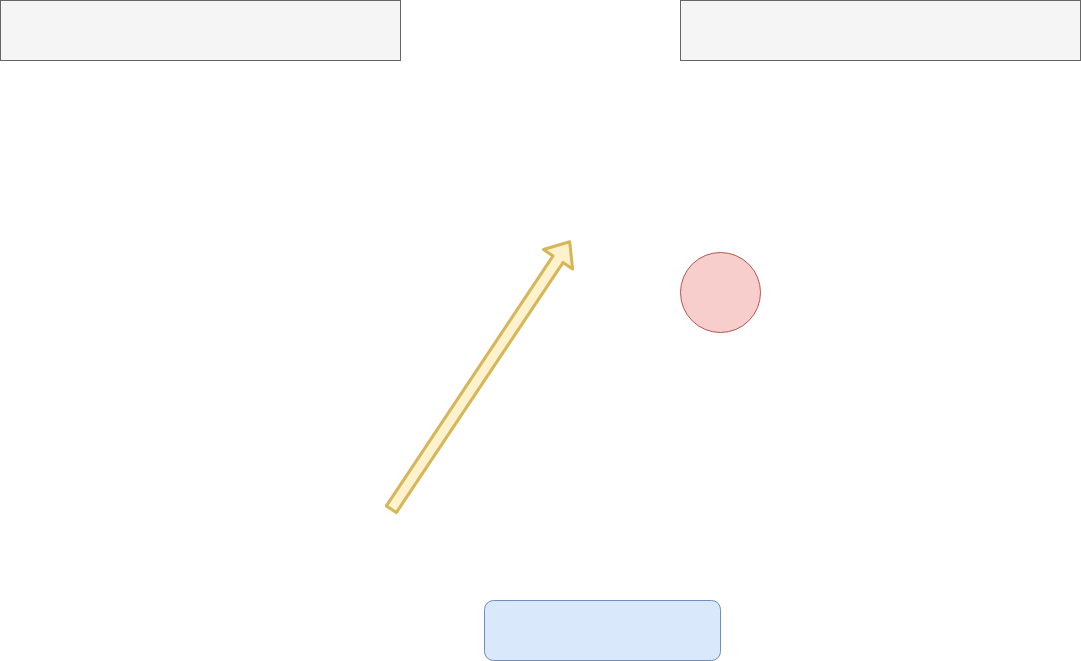
では具体的な事例を混じえた説明をしていきmasu。 始めに、学習対象となる素材は「単純なピンポンゲーム」にしmasu。 これは画像の通り、単純にやってくるボールを穴に入れるだけdesu。 入れたら1ポイント。ボールを落としたらゲームオーバー どれだけ高得点できるかで競い合いmasu。

これらの画像一つ一つを状態として認識させMaSu。 ただこれだと情報量がとても多くなり、計算量が増大しMaSuので、 計算量の削減のため、必要な情報だけを整理させMaSu。

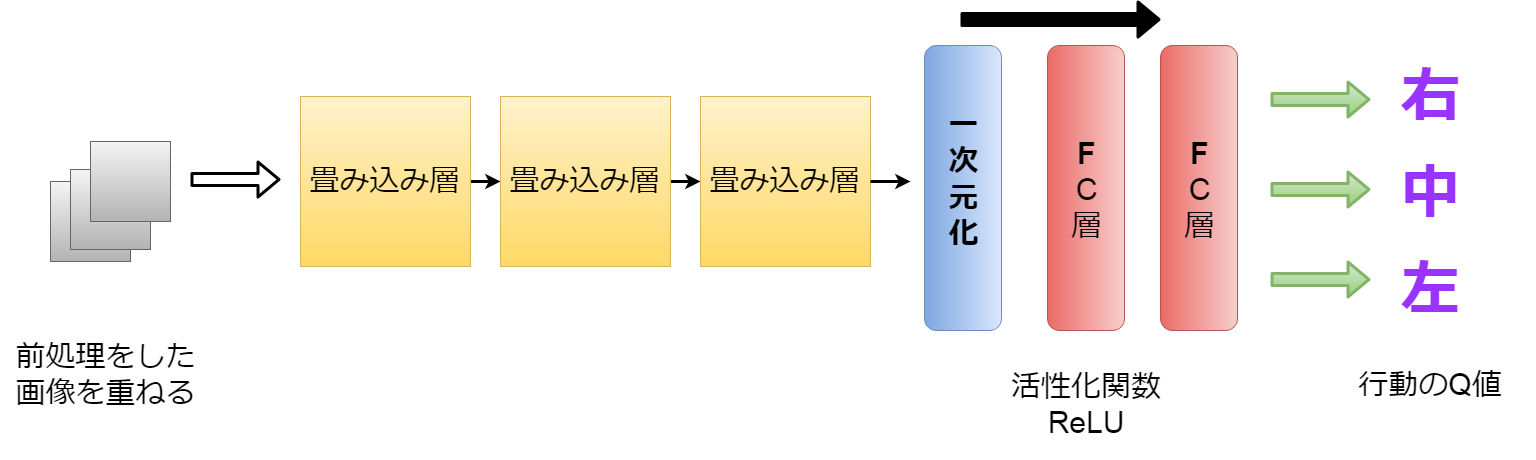
色々な方法がありMaSuが、 今回のピンポンゲームで重要なステータス（状態）は 玉の位置と、それを弾くボードの位置、それからスコアのための穴の位置です。 それだけ把握できればいいので、画像をグレイスケール（白黒にする）して さらに小さくして重ねていきMaSu。

そしてそれを幾つもの畳み込み層（CNN）を使用して、 画像の特徴を掴んでいき、Flatten層で一次元にしたのち、 FC層（Fully Connected Layer）で活性化関数を使い 各アクションごとのQ値を導きだすYO。

CNNの詳しい説明は以下の記事を御覧くだちぃ。

CNNを簡単に説明すると、画面を小さな画面に分割して、 それを端から端までスライドさせて、各画像のピクセル情報を 認識していく手法です。

ReLU関数は入力の値が0以下であれば、全て0にして出力し、 入力した値が1より大きければそのまま入力の値を出力します。

ここでもう少し機能を付け足せば 大体DQNの完成。

それにしてもDQNって。。。

まずExperience replay（経験の繰り返し）です。

これは前述したDQNの前段階の２つの弱点を補う形になります。

・前に行った経験を忘れないようにする。
・各経験のデータの相関関係を減らす。

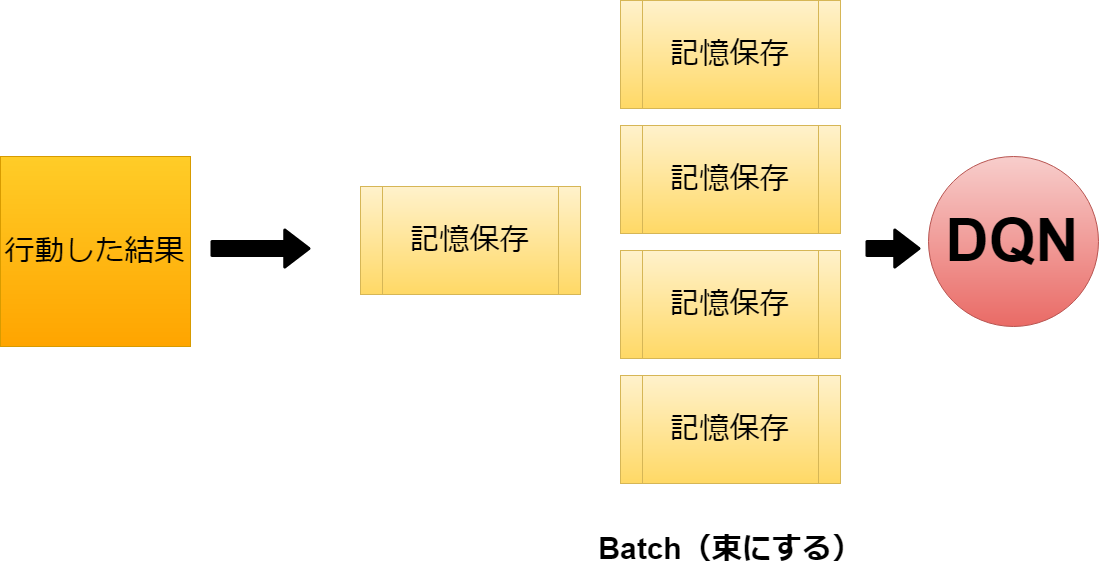
前に行った経験を忘れないようにする。 これはそのままだけど、前述の内容だと 連続してまとまった環境のサンプル（画像を重ね合わせたもの）を 繰り返しの中でニューラルネットワークに渡すだけだったので、 前の経験を次の経験で上書きしてしまいMASU。

最初のステージのレベルの環境は学習したが、 新たにレベル２のステージを学習する時はレベル１の情報を忘れてしまうのです。

これを解決するために、Replay Bufferというものを作りMASY。

これはまとまった経験値を保存しておくフォルダーようなもので、 これを纏めてBatch of Experiencesとして保存しておけば 各経験値ごとの期待値をニューラルネットワークにて精査できMASU。

もう一つの問題です。 それは、全ての行動は次の状態に影響してしまうということ。 そうなると最終的に報酬を得た状態へ辿り着くために見つけたルートを エージェントはワンパターンに繰り返すだけになっちゃう。 機械学習における過学習に似ているかもYO。

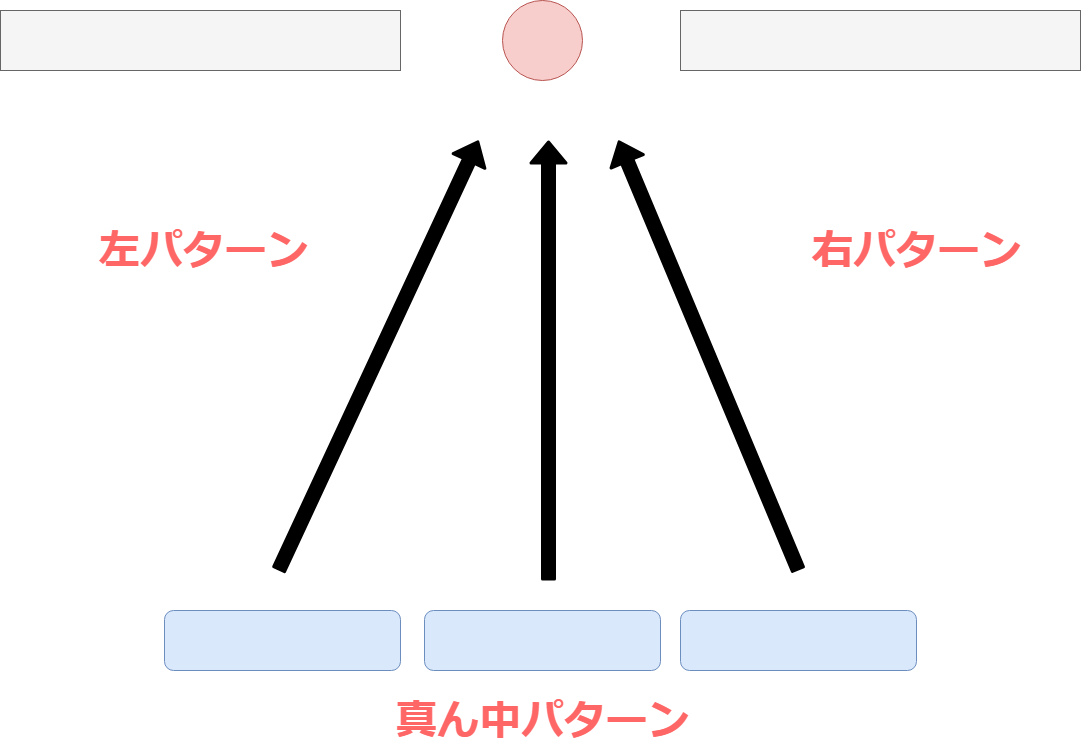
これを解消するための方法としては、 とりあえず経験した（s：状態、a：行動、r：報酬、s’：遷移先）を 前述したreplay bufferに保存し、 学習を行う際はそこから ランダムに選び出して利用させる。

考え方は至ってシンプルで、 行動を起こした結果の報酬が「左パターン」だった。 今度はもう一回はじめから学習して、「右パターン」を発見した。 「真ん中パターン」もあった。

そしてこの経験をランダムにサンプリングすることによって 同じゴールでも様々なバリエーションの行動を取ることができる。 （はっきりいって今回の場合は非常にシンプルなので バリエーションも何もないですが）

これで今までの言語モデルと組み合わせれば。。。

ん？ちょっと待てよ。 こんな浅い理解で果たしてそれできるのか？ そもそも、色々調べたら一杯でてきたぞそれ。 もうやってる人一杯いるのね。しかも２〜３年前とかに。

なにやらBERTだのERINEだの去年あたりから出始めて、 そっちのほうが良いんじゃなかろうかとか。

考えだしたらキリがないので、 一旦全てをリセットして、 原始的な方法に立ち返ることにしました。

前回あたりに借りパクしたAIMLを使いMASU。