Python Scriptと一緒に理解するCNN（Convolutional Neural Networks）の仕組み 最適化編
How CNN (Convolutional Neural Networks) Works with Python Scripts ~ Optimization ~

画像認識シリーズ第18弾です。前回のブログ記事。

This is the 18th image recognition series. Last blog post.

前回は勾配法の図による説明をおこないました。

In a previous my blog post, I explained the gradient method along with diagrams.

今回の記事は最適化についての説明をしていきます。

In this blog post, I'm going to briefly talk about optimization.

この手のものはやり尽くされていますが、ただ一から全部やってみたかった。それだけです。 つーことで今回は最適化について解説していきたいと思いMASU。

This kind of thing is done by many people, but I just wanted to do it all from scratch. That's all. Anyway, I would like to explain about optimization this time.

確率的勾配降下法のおさらいです。 あるゆる場所からボールを落とせるようにデータをミニバッチに分けて、ランダムに落とすイメージを描きました。

This is a review of the stochastic gradient descent method. I drew an image of randomly dropping the ball by dividing the learning data into mini batches so that the ball can be dropped from any place.

これはボールが転がる様子を上から見た図です。実際はこのように上手く事は運びません。

This is a gif image of the ball rolling from the top of the valley. The actual parameter update does not work this well.

基本的な確率勾配降下法（SGD）は、勾配を見つけると、次のように移動しながらパラメータを更新します。

The basic stochastic gradient descent (SGD) method finds the gradient and updates the parameters while moving as follows.

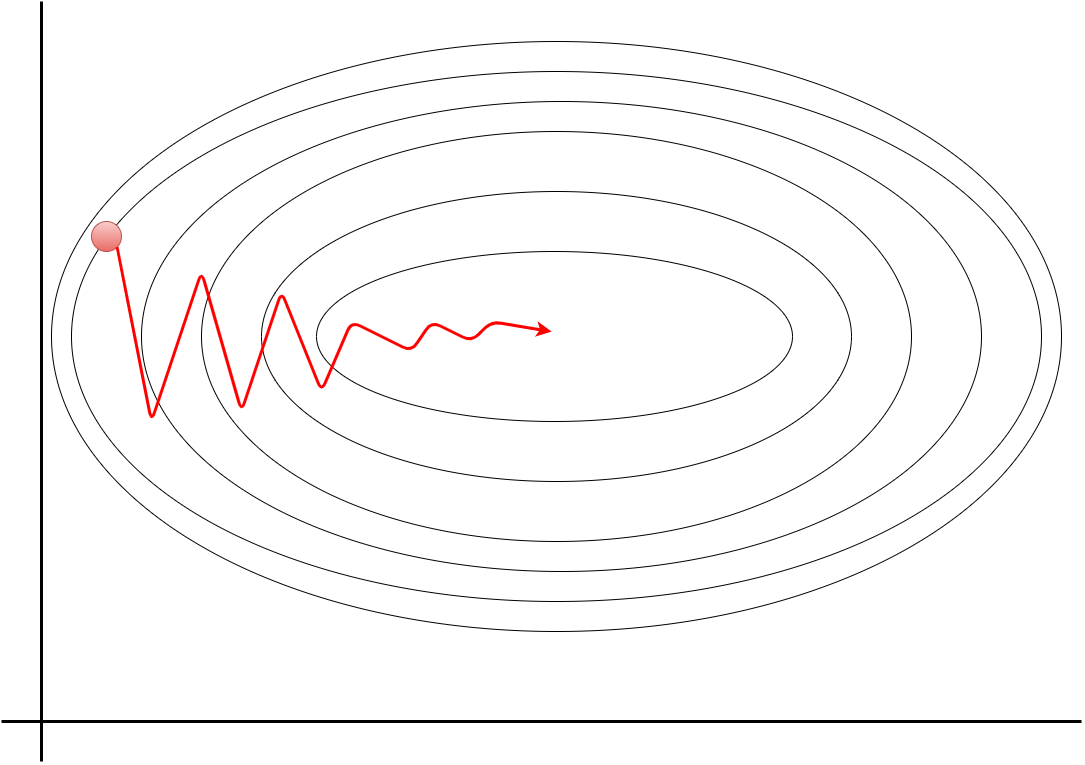
実はこのジグザグに移動することがとても非効率になります。

Actually, moving in this zigzag is very inefficient.

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-1, 1, 0.01)
y = np.arange(-1, 1, 0.01)

X, Y = np.meshgrid(x, y)
Z = (X**2)/30 + (Y**2)/3

cont = plt.contour(X,Y,Z,colors=['r', 'g', 'b'])
cont.clabel()

plt.xlabel('X')
plt.ylabel('Y')

plt.show()

X軸が水平方向に長い場合を考えてみます。

Suppose the X axis is long horizontally.

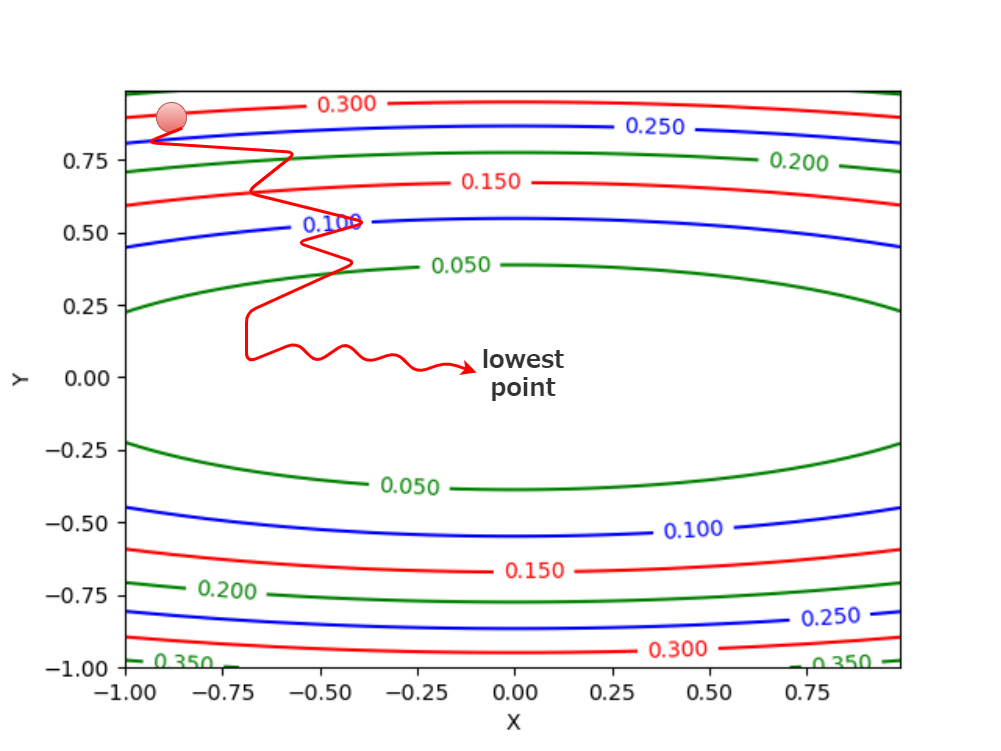
この非効率さの原因は、本来の「一番低いポイント」への勾配方向ではない方向に進もうとするためです。 最初の等高線の高さ「0.300」から次の「0.250」へ進むのに、X軸が横に長く伸びているため、 とにかく近場の低い方向に進んでから、また計算して反転するといったことをしています。結果ジグザグな動きになります。

This inefficiency is caused by an attempt to go in a direction that is not the gradient to the "lowest point". The ball moves from the first contour line "0.300" to the next contour line "0.250" nearby. However, because the X axis extends horizontally so long that it rolls in the lower direction of the near field before rolling to its original lower position, it rolls in the lower direction of the near field, changing direction many times, resulting in a zigzag motion.

これを解消するのにMomentumという物理の考えを利用します。

To solve this problem, we use a physics concept called momentum.

Momentumを簡単に理解するために以下のGIF画像を見てください。

To make momentum easier to understand, check out the GIF image below.

実際のボールは急斜面の下方向に対してどんどん速度を上げて転がります。 ところが上方向の傾斜や地面の摩擦、空気抵抗によって減速し、やがて平らな地面の上で止まります。

A real world ball rolls faster and faster down the steep slope. However, the ball slows down due to ground friction, air resistance, and gravity, causing it to stop on flat place.

このようにMomentumを適用して、複雑な谷をボールが転がろうとする様子をイメージしてください。

Use momentum in this way to visualize a ball rolling down a complex valley.

①で勾配を見つけて下方向に転がります。

① The ball senses the gradient and rolls down.

②でMomentumが働き、傾斜に押し戻されます。

② Momentum acts on the ball and it tries to advance to the next gradient.

③また勾配を見つけて下方向に転がります。

③ The ball also detects the gradient and rolls down again.

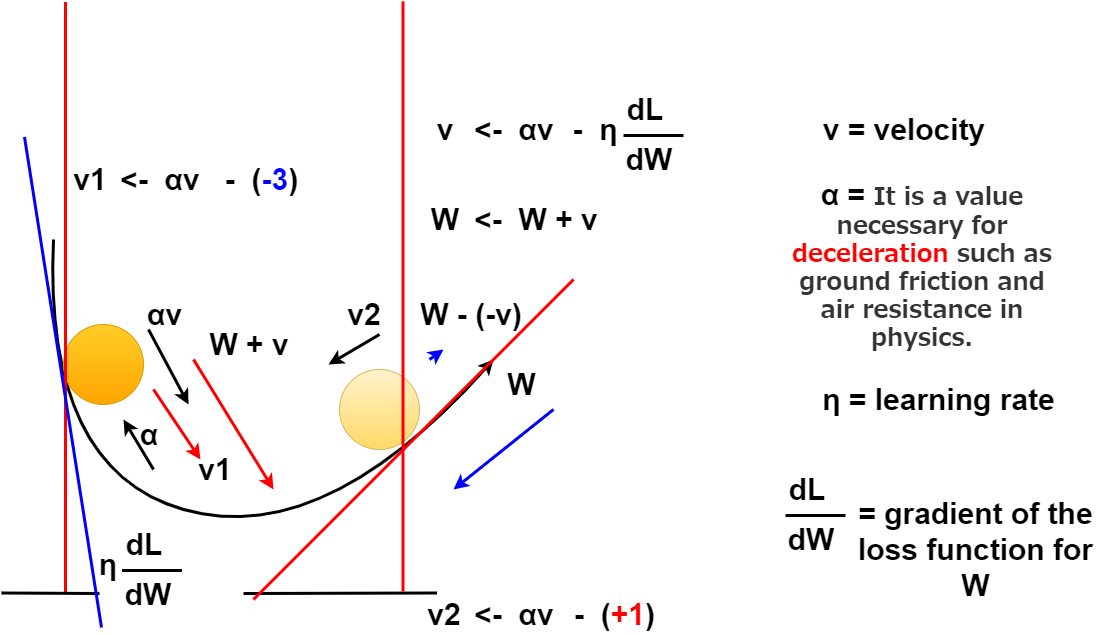
またもやごちゃごちゃしてすみません。 要は勾配が負の方向に傾いていて、傾きが大きければ 更新するパラメーターはどんどん大きくなります。（加速していく。）

Sorry for the mess diagram again. In short, if the gradient is tilted in the negative direction and the slope is large, The updated parameter value increases. (It's like a acceleration.)

ボールが坂を下りきって、登って行ってしまっても、勾配が正の方向に傾いていて、傾きが大きければ徐々に重みパラメーターの値は少なく更新されていき、 マイナスになったら、ボールは損失値（グラフでいう曲線）がゼロの方向に引き戻されます。 ちなみにαが小さいほど、傾斜の影響（勾配の大きさ）を大きく受けます。

If the ball is goes all the way down the gradient and tries to climb it again. If the slope is inclined in a positive direction and the slope is large, The weight parameter value gradually decrease. Eventually, the weight parameter value changes to a negative value, and the ball tries to fall back near the loss value (curve of the graph) of 0. Incidentally, the smaller α is, the greater the influence of the inclination (gradient magnitude).

等高線の図で表すとボールは以下の様な動きになります。

In a contour plot, the ball moves as follows.

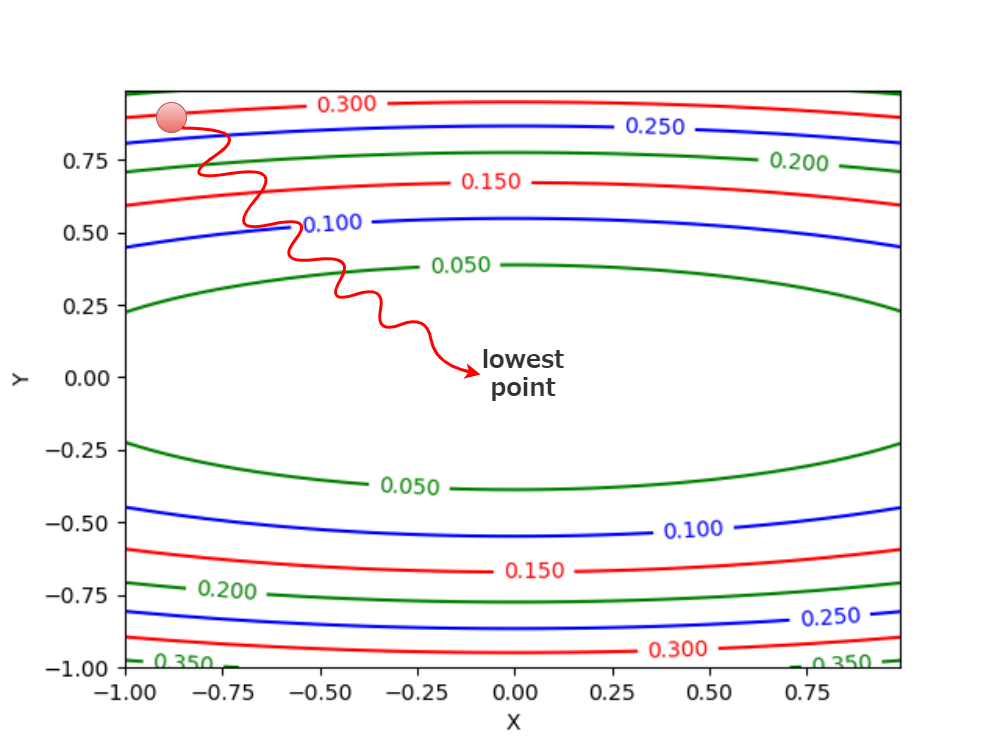
軽くPythonで試してみましょう。

Just try it out in Python

import numpy as np

def func1(x):
    return x**2 + 1

def func2(params):
    return np.sum(np.power(params,2))

def differentiation(f, x):
    h = 1e-7
    return (f(x + h) - f(x - h)) / (2*h)

def gradient(f, params):
    h = 1e-7
    grad = np.zeros_like(params)
    for idx in range(params.size):
        tmp_val = params[idx]
        params[idx] = tmp_val + h
        fxh1 = f(params)
        params[idx] = tmp_val - h
        fxh2 = f(params)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        params[idx] = tmp_val
    return grad

def desc_meth(f, init_x, lr=0.01, step=100):
    x = init_x
    for i in range(step):
        slope = differentiation(f, x)
        x -= lr * slope
    return x

def grad_desc_meth(f, init_params, lr=0.01, step=100):
    params = init_params
    for i in range(step):
        grad = gradient(f, params)
        params -= lr * grad
    return params

def momentum(lr, a, v, params, grads):
    new_params = params
    for grad in grads:
        v = a*v - (lr * grad) 
        new_params += v
    return new_params

lr = 0.01
a = 0.9
v = 0
params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = momentum(lr, a, v, params, grads)

次の最適化手法として学習係数の減衰があります。

The next optimization algorithm is to attenuate the learning rate.

これはAdaGradといって、今まで学習率は一定にして計算していたが、パラメータ一つ一つに対して学習率を調整していけるようにしたものです。

This is called AdaGrad, and although the learning rate has been calculated at a constant level until now, the learning rate can be adjusted for each parameter.

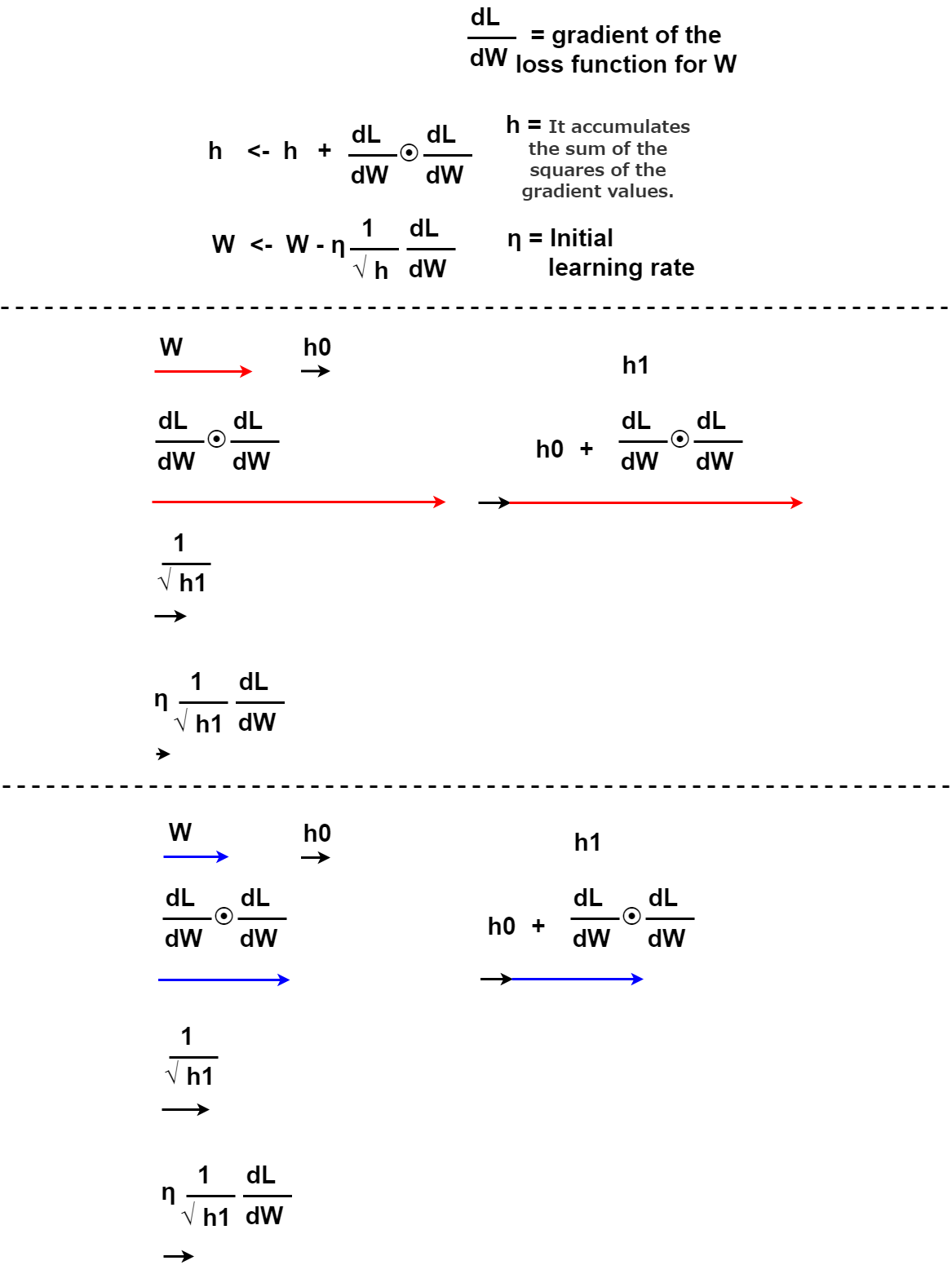
この図の通り、要するに大きく変動したパラメータには次回から小さい学習率をかけていけるということです。

As you can see in this figure, in short, you can apply a small learning rate to the parameter that has changed greatly from the next time.

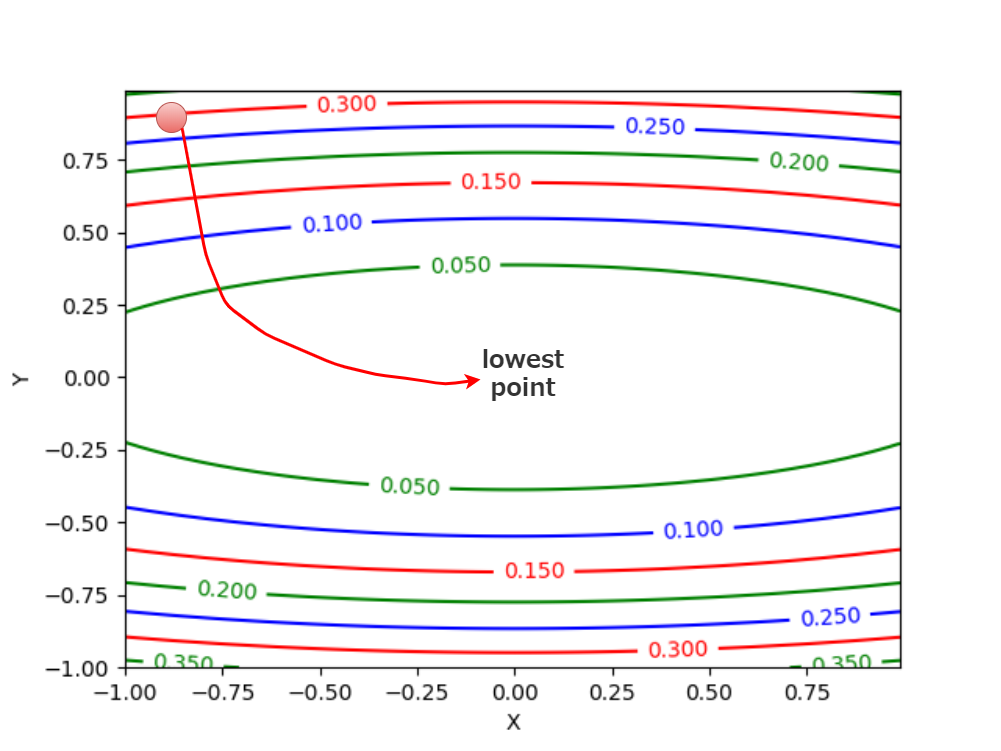
この図のようにAdaGradは最初は大きい学習率を設定して、大きく勾配に沿ってボールを動かしていき、徐々に動く距離を小さくしていけば、より効率的に関数の最小値に辿り着けるだろうといった考え方です。

The idea of AdaGrad is that by first setting a high learning rate, move the ball along a large slope, and then move it down a small distance, the ball will be able to reach the minimum value of the function more efficiently.

軽くPythonで試してみましょう。

Just try it out in Python

def adagrad(lr, h, params, grads):
    eps = 1e-7
    new_params = params
    for grad in grads:
        h += grad * grad 
        new_params -= lr * grad / (np.sqrt(h) + eps)
    return new_params

lr = 0.01
h = 0
params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adagrad(lr, h, params, grads)

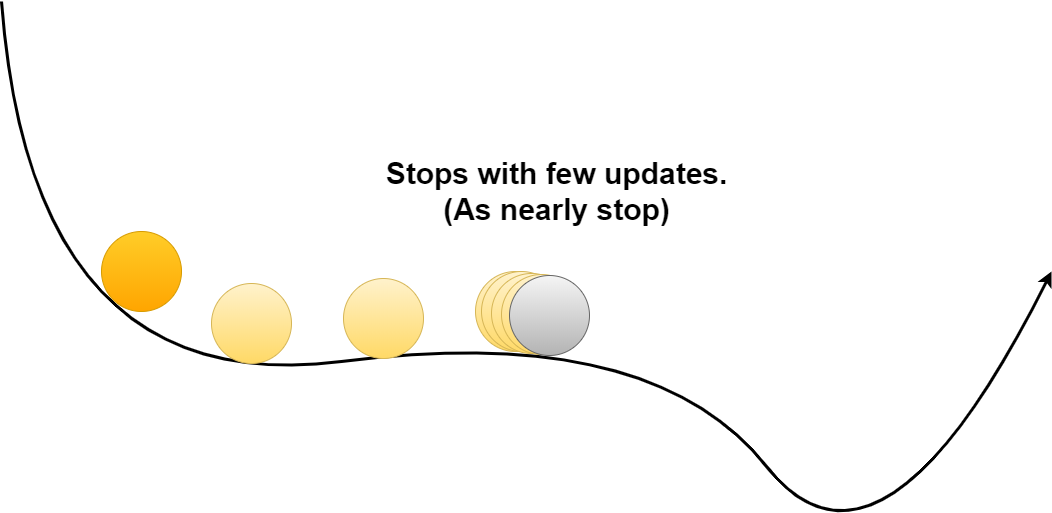
しかし、AdaGradは学習を進めれば進めるほど更新量が小さくなり、結果本当はもっと先に最小値がある場合にも学習がストップしてしまう場合があります。

However, With AdaGrad, the more learning, the fewer updates there are, and the closer to zero. This can cause learning to stop even if the minimum value is still ahead.

これを防ぐために過去の全ての勾配を均一に加算していくのではなく、指数移動平均を使って過去の勾配の情報を除々に少なくしていって、現在の勾配情報に重きを置くようにする手法を取り入れます。

To prevent this, instead of uniformly adding all the gradients in the past, we introduce a technique that uses an exponential moving average to gradually reduce the information of the gradients in the past and put more emphasis on the current gradient information.

軽くPythonで試してみましょう。

Just try it out in Python

def adagradEMA(lr, h, a, params, grads):
    eps = 1e-7
    new_params = params
    for grad in grads:
        h += (a * h) + (1 - a) * grad * grad 
        new_params -= lr * grad / (np.sqrt(h) + eps)
    return new_params

lr = 0.01
h = 0
a = 0.99

params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adagradEMA(lr, h, a, params, grads)

この指数移動平均を使った勾配スケールの減少とモーメンタムを上手く組み合わせたのがAdamです。

Adam is optimization algorithm that uses this exponential moving average to reduce the gradient scale, and incorporates the concept of momentum.

軽くPythonで試してみましょう。

Just try it out in Python

def adam(lr, m, v, eps, beta1, beta2, params, grads):
    
    new_params = params
    for i, grad in enumerate(grads):
        i += 1
        lr_t  = lr * np.sqrt(1.0 - beta2**i) / (1.0 - beta1**i)
        m += (1 - beta1) * (grads - m)
        v += (1 - beta2) * (grads**2 - v)
        
        new_params -= lr_t * m / (np.sqrt(v) + eps)
    return new_params

lr = 0.001
m = 0.0
v = 0.0
eps = 1e-8
beta1 = 0.99
beta2 = 0.999

params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adam(lr, m, v, eps, beta1, beta2, params, grads)

Adamが描くボールの軌跡の図は以下の様になります。

Adam's drawing diagram of the ball's trajectory is looks like this.

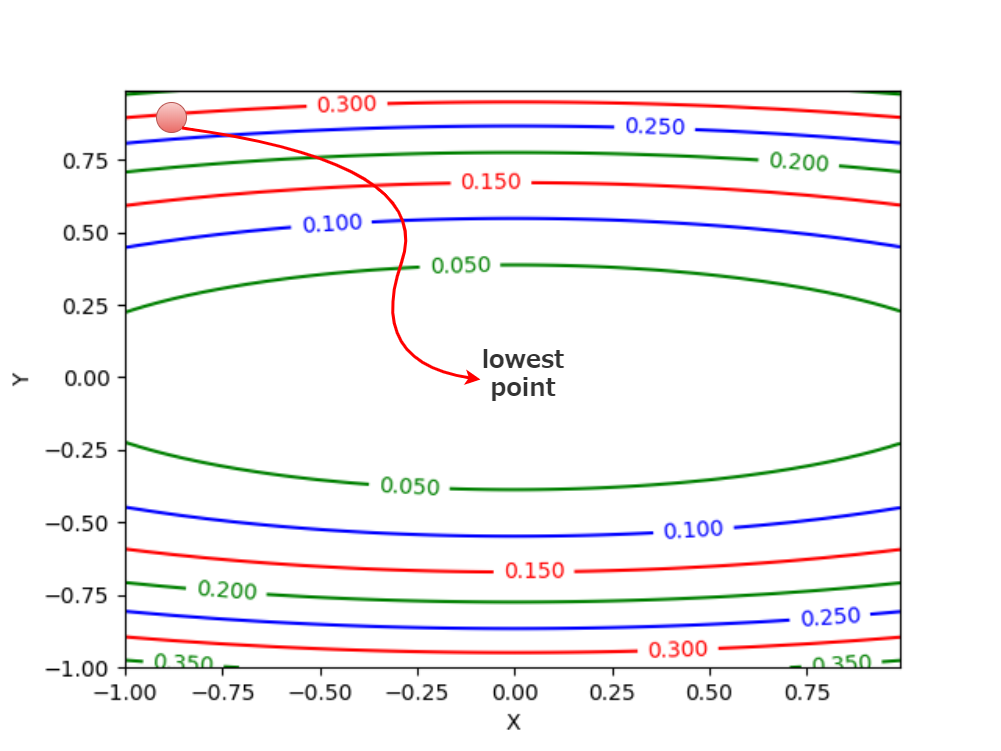
モーメンタムからAdamまでの出力の結果は以下のようになります。 ですが、Paramsはこんなに単純ではないですし、Gradsもそうです。

The output from momentum to Adam is as follows. But Parames is not this simple, and so is Grads.

lr = 0.01
a = 0.9
v = 0
params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = momentum(lr, a, v, params, grads)
  
Out: 
[3. 6.]
[ 6.         12.00000003]
[2.766 5.766]
[ 5.532      11.53200003]
[2.545572 5.545572]
[ 5.09114397 11.091144  ]
[2.33792882 5.33792882]
[ 4.67585764 10.67585767]
[2.14232895 5.14232895]
[ 4.28465789 10.28465793]
[1.95807387 4.95807387]
[3.91614774 9.91614778]
[1.78450559 4.78450559]
[3.56901117 9.5690112 ]
[1.62100426 4.62100426]
[3.24200853 9.24200856]
[1.46698602 4.46698602]
[2.93397203 8.93397205]
[1.32190083 4.32190083]
[2.64380166 8.64380167]

lr = 0.01
h = 0
params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adagrad(lr, h, params, grads)
  
Out: 
[3. 6.]
[ 6.         12.00000003]
[2.98105573 5.98105573]
[ 5.96211144 11.96211151]
[2.96210579 5.96210579]
[ 5.92421156 11.92421163]
[2.94315017 5.94315017]
[ 5.88630034 11.88630037]
[2.92418882 5.92418882]
[ 5.8483776  11.84837767]
[2.90522171 5.90522171]
[ 5.8104434  11.81044347]
[2.88624882 5.88624882]
[ 5.77249764 11.77249768]
[2.86727012 5.86727012]
[ 5.73454024 11.73454027]
[2.84828557 5.84828557]
[ 5.69657114 11.69657118]
[2.82929514 5.82929514]
[ 5.65859025 11.65859032]

lr = 0.01
h = 0
a = 0.99

params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adagradEMA(lr, h, a, params, grads)
  
Out: 
[3. 6.]
[ 6.         12.00000003]
[2.81828224 5.81828224]
[ 5.63656446 11.63656453]
[2.63571681 5.63571681]
[ 5.2714336  11.27143367]
[2.45224611 5.45224611]
[ 4.90449221 10.90449224]
[2.26780786 5.26780786]
[ 4.53561572 10.53561576]
[2.08233508 5.08233508]
[ 4.16467016 10.16467017]
[1.89575624 4.89575624]
[3.79151247 9.79151251]
[1.70799598 4.70799598]
[3.41599195 9.41599199]
[1.51897643 4.51897643]
[3.03795288 9.03795291]
[1.32861981 4.32861981]
[2.65723962 8.65723964]

lr = 0.001
m = 0.0
v = 0.0
eps = 1e-8
beta1 = 0.99
beta2 = 0.999

params = np.array([3.0, 6.0])

for i in range(10):
    print(params)
    grads = gradient(func2, params)
    print(grads)
    params = adam(lr, m, v, eps, beta1, beta2, params, grads)
  
Out: 
[3. 6.]
[ 6.         12.00000003]
[2.998 5.998]
[ 5.996      11.99600007]
[2.996 5.996]
[ 5.992      11.99200003]
[2.994 5.994]
[ 5.988      11.98800003]
[2.992 5.992]
[ 5.98399996 11.98400003]
[2.99 5.99]
[ 5.98       11.98000003]
[2.988 5.988]
[ 5.976      11.97600003]
[2.986 5.986]
[ 5.972      11.97200003]
[2.984 5.984]
[ 5.96799996 11.96800003]
[2.982 5.982]
[ 5.964      11.96400007]

X,Yは画像がフィルタリングされたものが幾つも重なったものの入力と出力で、 途中で全結合層によって膨大な数の重みパラメータが掛けられます。 そして普通の二次関数の代わりに損失関数が入ります。

X, Y are the inputs and outputs of multiple images filtered. Along the way, the Fully Connected Layers multiplies an enormous number of weight parameters. Then, instead of the usual quadratic function, we have a loss function.

まあ兎に角、これで単純なCNN学習モデルがやっとできました。

Anyway, now we have a simple CNN learning model.

opt = keras.optimizers.adam()

model.compile(loss='categorical_crossentropy',
            optimizer=opt,
            metrics=['accuracy'])

model.fit(X,y,batch_size=batch_size, epochs=epochs)

ということで、お次は学習モデルの簡単なおさらいですDESU。

In the next blog post, I'm going to write about a quick review of the learning model.