Python Scriptと一緒に理解するCNN（Convolutional Neural Networks）の仕組み Categorical Cross-Entropy編
How CNN (Convolutional Neural Networks) Works with Python Scripts ~ Categorical Cross-Entropy ~

画像認識シリーズ第13弾です。前回のブログ記事。

This is the 13th image recognition series. Last blog post.

前回はmodel_train関数内のSoftmaxの図による説明をおこないました。

In a previous my blog post, I explained about Activation Function Softmax, along with diagrams.

それと前回は次回にOptimizer Adamの説明を予定と書きましたが、 Cross-Entorpy errorの説明を忘れていたので、今回の記事は SoftmaxとCross-Entropyを組み合わせたCategorical Cross-Entorpyの説明をしていきます。

Also, In my previous blog post, I mentioned that I would like to explain Optimizer Adam next time. But I forgot to mention about Cross-Entoropy error, So in this blog post, I'm going to talk about Categorical Cross-Entropy that the combination of Softmax and Cross-Entropy.

この手のものはやり尽くされていますが、ただ一から全部やってみたかった。それだけです。 つーことで今回はCategorical Cross-Entropyに関してを解説していきたいと思いMASU。

This kind of thing is done by many people, but I just wanted to do it all from scratch. That's all. Anyway, I would like to explain about Categorical Cross-Entropy this time.

Categorical Cross-Entropyの簡単な趣旨です。

A quick overview of Categorical Cross-Entropy.

今回説明するCategorical Cross Entropyは、前回説明したSoftmax関数にCross-Entropy-error関数をくっつければ完成します。

Categorical Cross Entropy, which I'm going to describe in this blog post, is a combination of the Cross-Entropy-error function and the Softmax function described in my previous blog post.

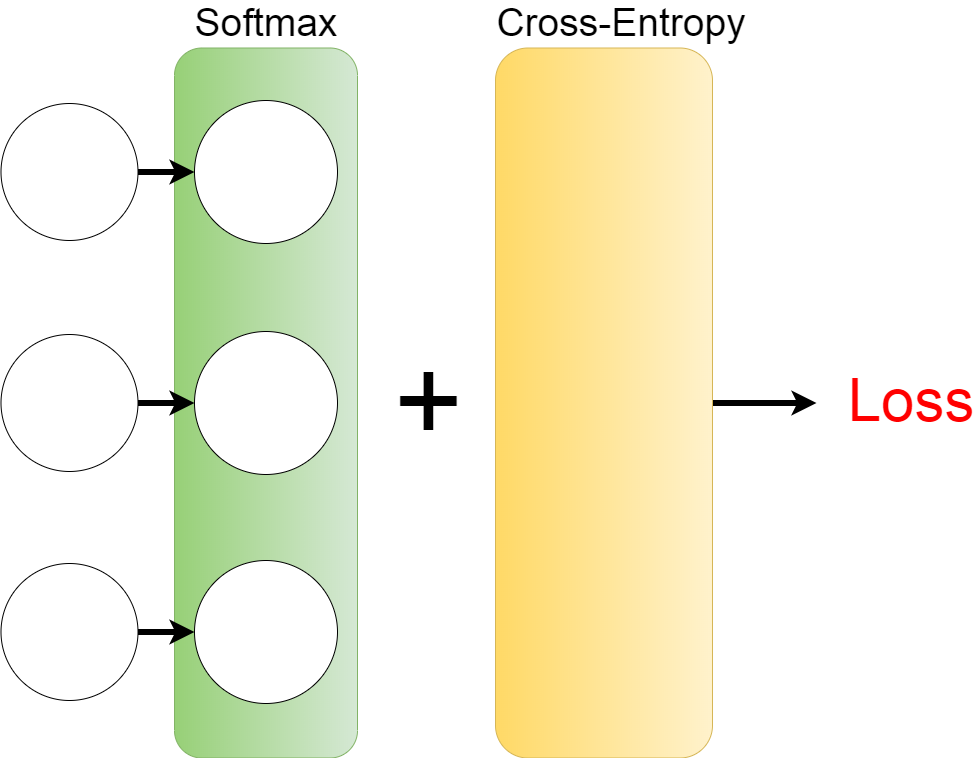
このCross-Entropy-errorは損失関数と言われるもので、上の図のLoss（損失）を計算してくれます。

The Cross-Entropy is called a loss function, and it calculates Loss (loss) in the figure above.

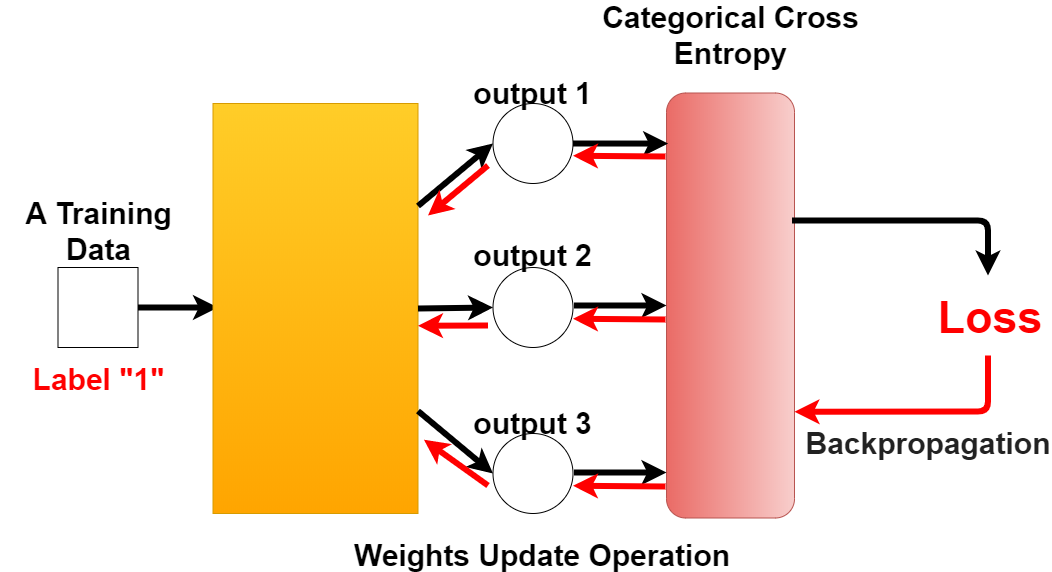
上の図から、Categorical Cross Entropyを使うと正解ラベルとなる出力の結果で損失値が計算できるようになるのです。

As you can see in the diagram above, Categorical Cross Entropy allows you to calculate the loss value with the result of the output that gives the correct label.

損失値が計算できれば、weightと呼ばれる値を調整することによって、より正しい学習ができるようになります。

Once the loss value is calculated, the percentage of correct answers can be increased by adjusting the value called weight.

では趣旨を踏まえた上でCategorical Cross Entropy自体を簡単に説明します。

Let's take a quick look at Categorical Cross Entropy itself based on the purport.

取り敢えず全体のコードは以下になります。

For now, the whole script is as follows.

Improved version of cifar10_cnn.py

imp_ver_cf10cnn.py

import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.utils import np_utils
import numpy as np


labels = ["dogs", "cats", "monkeys", "birds", "fish", "lizards"]
total_num = len(labels)
image_size = 100

batch_size = 32
epochs = 100

def main():
    X_train, x_test, Y_train, y_test = np.load("data/augumented_images.npy")
    X_train = X_train.astype("float") / 256
    x_test = x_test.astype("float") / 256
    Y_train = np_utils.to_categorical(Y_train, total_num)
    y_test = np_utils.to_categorical(y_test, total_num)

    model = model_train(X_train, Y_train)
    model_eval(model, x_test, y_test)

def model_train(X, y):
    model = Sequential()
    model.add(Conv2D(32, (3, 3), padding='same',
                    input_shape=X.shape[1:]))
    model.add(Activation('relu'))
    model.add(Conv2D(32, (3, 3)))
    model.add(Activation('relu'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Dropout(0.25))

    model.add(Conv2D(64, (3, 3), padding='same'))
    model.add(Activation('relu'))
    model.add(Conv2D(64, (3, 3)))
    model.add(Activation('relu'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Dropout(0.25))

    model.add(Flatten())
    model.add(Dense(512))
    model.add(Activation('relu'))
    model.add(Dropout(0.5))
    model.add(Dense(total_num))
    model.add(Activation('softmax'))

    opt = keras.optimizers.adam()

    model.compile(loss='categorical_crossentropy',
                optimizer=opt,
                metrics=['accuracy'])
    
    model.fit(X,y,batch_size=batch_size, epochs=epochs)

    model.save("data/creatures_cnn.h5")

    return model

def model_eval(model, X, y):
    scores = model.evaluate(X, y, verbose=1)
    print('Test Loss', scores[0])
    print('Test Accuracy', scores[1])

if __name__=="__main__":
    main()

Categorical Cross Entropyはmodel.compileの中の引数に指定されています。

Categorical Cross Entropy is specified as an argument in model.compile.

model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

まずCross Entropy Errorの数式はこのようになっています。

First, the formula for Cross Entropy Error looks like this.

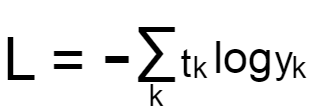
上の式を図にすると以下になります。

The above expression is illustrated as follow.

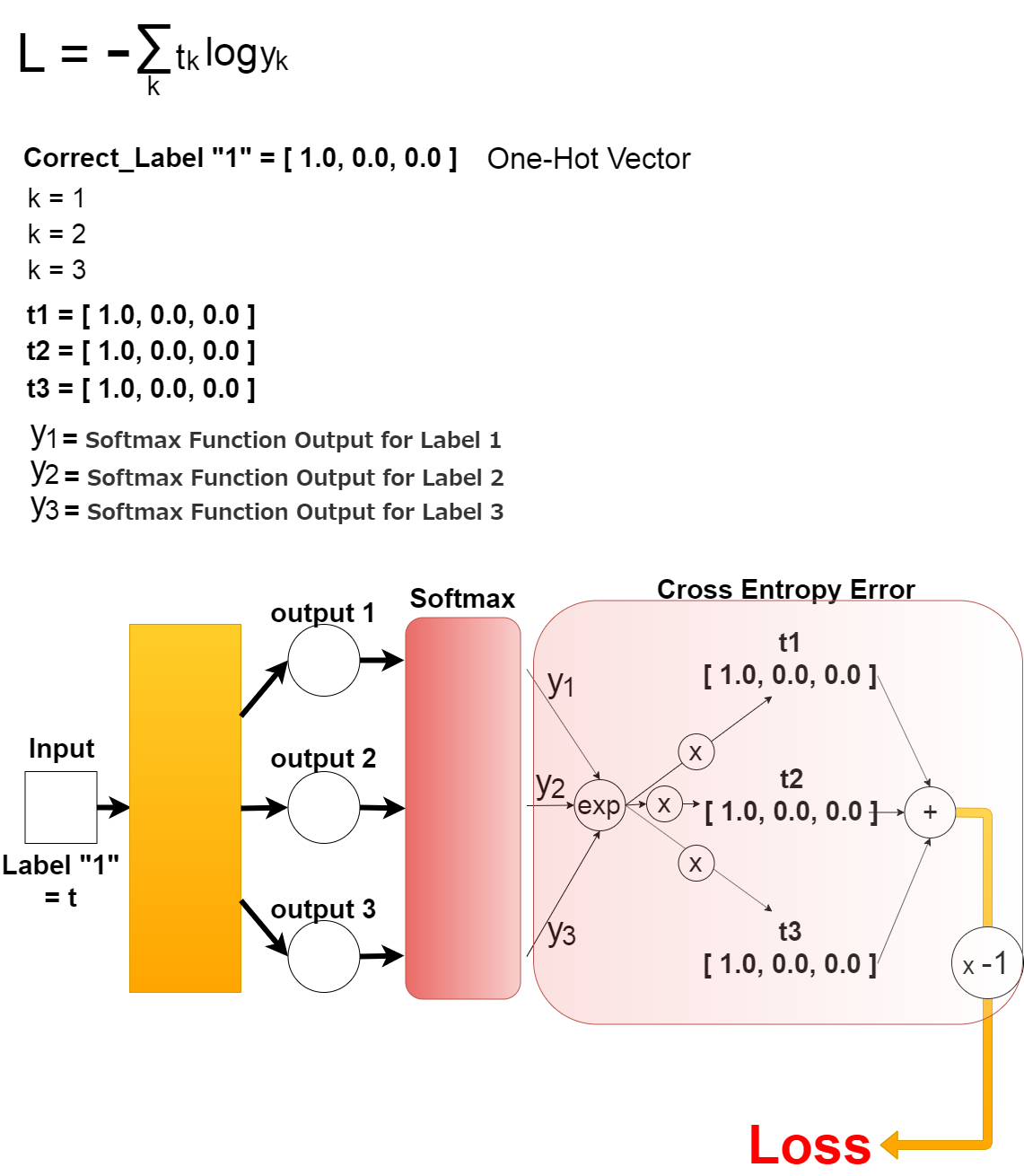
Pythonで簡単な例を元に計算してみましょう。

Let's do the math using a simple example in Python.

import numpy as np
output_by_softmax_1 = np.array([0.012, 0.18, 0.033, 0.775])
output_by_softmax_2 = np.array([0.12, 0.18, 0.33, 0.37])

correct_label = np.array([0.0, 0.0, 0.0, 1.0])

クラス（ラベル）が4つ、正解ラベルは”4番目”だったとする。 output_by_softmax_1は高い正解率。 output_by_softmax_2は低い正解率。

Suppose you have 4 classes (labels) and the correct label is "4th". output_by_softmax_1 is a high percentage of correct answers. output_by_softmax_2 is a low percentage of correct answers.

In [6]: -np.log(output_by_softmax_1)
Out[6]: array([4.42284863, 1.71479843, 3.41124772, 0.25489225])

In [6]: -np.log(output_by_softmax_2)
Out[6]: array([2.12026354, 1.71479843, 1.10866262, 0.99425227])

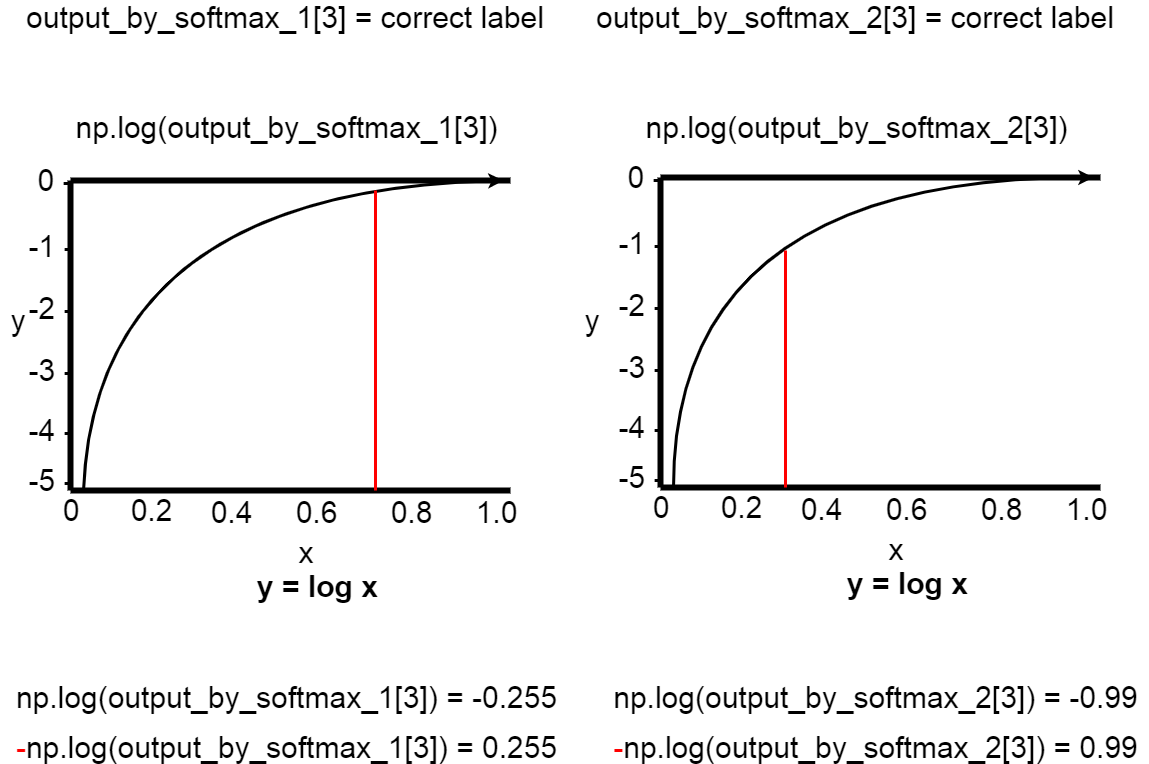
正解率が高いほど、np.log(output_by_softmax)の結果は0に近づく。

The higher the accuracy, the closer the np.log(output_by_softmax) result is to 0.

In [41]: -1*np.sum(np.log(output_by_softmax_1).dot(correct_label))
Out[41]: 0.25489224962879004

In [42]: -1*np.sum(np.log(output_by_softmax_2).dot(correct_label))
Out[42]: 0.9942522733438669

output_by_softmax_1の正解ラベルの出力は「0.775」。 結果は0.25489224962879004。 output_by_softmax_2の正解ラベルの出力は「0.37」。 結果は0.9942522733438669 正解率が高いほど、出力結果は0に近づくので、正しく計算ができている。

The correct label output for output_by_softmax_1 is "0.775". The result was 0.25489224962879004. The correct label output for output_by_softmax_2 is "0.37". The result is 0.9942522733438669. The higher the percentage of correct answers, the closer the output is to zero, so the correct calculation was made.

これで”model.compile”の”loss=”と”metrics=['accuracy']”までが終わりました。

This completes the "loss=" and "metrics=['accuracy']" in "model.compile".

model.compile(loss='categorical_crossentropy',
            optimizer=opt,
            metrics=['accuracy'])

これまでの全体像です。

This is an overall diagram.

model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
                input_shape=X.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(total_num))
model.add(Activation('softmax'))

opt = keras.optimizers.adam()

model.compile(loss='categorical_crossentropy',
            optimizer=opt,
            metrics=['accuracy'])

残りの説明は次回に持ち越します。お次はbatch_sizeとepochsの説明を予定してます。Optimizerの説明はその後のほうが良いと思います。

I will carry over the rest of the explanation next time. Next comes about "batch_size" and "epochs". I think Optimizer should be discussed later.

See You Next Page!