Published Date : 2019年12月27日23:27

p5.jsとnumjs - コサイン類似度
p5.js and numjs - Cosine Similarity

This blog has an English translation

今回の記事は、p5.jsとnumjsを使って自然言語処理のコサイン類似度を試したいと思います。

In this article, I'll try a Cosine Similarity in natural language processing using p5.js and numjs.

もちろん、P5はJavascriptで作られているので、P5内でJavascriptそのものが使えます。なので、基本P5で書いていきますが、P5では難しい文字列処理等はJavascriptでそのまま書いていきます。

Of course, p5.js is written in Javascript, so you can use it directly in p5.js. I usually write code in p5.js, but there many things that are difficult to process in p5.js (String operations, etc.), so if I encounter such a situation, I write code directly in Javascript.

目次
Table of Contents

概要

Summary

コサイン類似度

Cosine Similarity

ページの最後へ

Go to the end of the page.

概要
Summary

簡単な概要です。

Here's a quick overview.

まずこの記事の趣旨は、 NumjsというNumpy(Python)のJavascriptヴァージョンを使用して、 ML.js等のライブラリを使わずにできるだけ１から自然言語処理の仕組みを理解することです。

First of all, the purpose of this blog post is use Numjs that a Javascript version of Python's Numpy, to understand how natural language processing works, without using libraries like ML.js.

機械学習用のライブラリを使えば簡単に事は進みますが、少しでも細かくその仕組みを知っておけば、色々なことに応用できると思います。

If you use a library for machine learning, things go easy, but I think if you know how the details of how machine learning works, you can apply it to many things.

今回はこの記事で簡単に説明したコサイン類似度を使って、単語の類似度を調べるスクリプトを作りたいと思います。

This time, I'll use the cosine similarity I briefly described in this blog post to create a script to check the similarity of words.

コサイン類似度
Cosine Similarity

コサイン類似度を計算する式は以下の通り。

The formula for calculating cosine similarity is as follows.

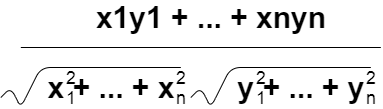
コサイン類似度とは、簡単に言うと、２つのベクトルが完全に同じ方向を向いていれば「1」、逆向きであれば「-1」という数字を計算します。

Briefly, the similarity of the cosines is calculated as the number 1 if the two vectors are pointing in exactly the same direction, or the number -1 if they are pointing in the opposite direction.

より直感的に理解するためには、下に示した図の通り、単語をベクトルとして表現した場合の矢印の方向が、コサイン類似度を表している。

For a more intuitive understanding, as shown in the figure below, the direction of the arrow when a word is expressed as a vector represents the cosine similarity.

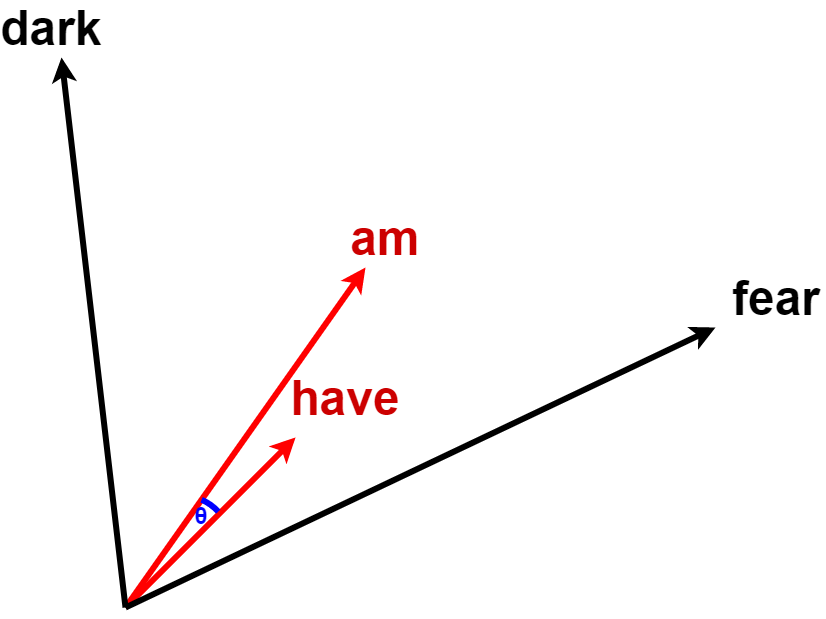
では計算式をp5に直してみます。

Let's change the formula to p5.

cosSimilarity.js

function cosSimilarity(x, y){
    let nx = x.divide((nj.sqrt(nj.sum(x.pow(2))).add(Number.EPSILON)).get(0));
    let ny = y.divide((nj.sqrt(nj.sum(y.pow(2))).add(Number.EPSILON)).get(0));
    
    return nj.dot(nx, ny);
}

Number.EPSILONはゼロ除算を防ぐためのとても小さい数です。（例：1e-10 = 0.0000000001）

Number.EPSILON is a very small number to prevent division by zero. (Example: 1e-10 = 0.0000000001)

HTMLファイルにJSのパスを追加してくだちぃ。

Add the JS path to your HTML file.

working folder

your working directory
    -- assets
        -- sixLittleMice.txt
    -- nlpExample.html
    -- nlpExample.js
    -- utils
        -- preprocess.js
        -- buildCoOccurrenceMatrix.js
        -- cosSimilarity.js

nlpExample.html

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <meta http-equiv="X-UA-Compatible" content="ie=edge">
    <!-- p5.js cdn -->
    <script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.6.1/p5.min.js"></script>
    <script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.6.1/addons/p5.dom.min.js"></script>
    <!-- numjs cdn -->
    <script src="https://cdn.jsdelivr.net/gh/nicolaspanel/[email protected]/dist/numjs.min.js"></script>
    <!-- utils -->
    <script src="../../utils/preprocess.js"></script>
    <script src="../../utils/buildCoOccurrenceMatrix.js"></script>
    <script src="../../utils/cosSimilarity.js"></script>
    <!-- sketch -->
    <script src="nlpExample.js"></script>
    <title>Document</title>
</head>
<body>
</body>
</html>

試しに使ってみましょう。

Let's try it.

let text = ["a b c d e c b a"]
let result = preprocess(text)

let corpus = result[0];
let word2Id = result[1];
let id2Word = result[2];

print("corpus", corpus);
print("word to id", word2Id);
print("id to word", id2Word);
`
corpus
(8) [0, 1, 2, 3, 4, 2, 1, 0]
word to id
{a: 0, b: 1, c: 2, d: 3, e: 4}
id to word
{0: "a", 1: "b", 2: "c", 3: "d", 4: "e"}
`

let vocabSize = Object.keys(word2Id).length;
print(vocabSize)
// 5
let CM = buildCoOccurrenceMatrix(corpus, vocabSize);
print('co occurrence matrix', CM.tolist());

`
co occurrence matrix
0: (5) [0, 1, 0, 0, 0]
1: (5) [1, 0, 1, 0, 0]
2: (5) [0, 1, 0, 1, 1]
3: (5) [0, 0, 1, 0, 1]
4: (5) [0, 0, 1, 1, 0]
`

let d = CM.tolist()[word2Id['d']]
print('d vector', d)
// e vector[0, 0, 1, 0, 1]
let b = CM.tolist()[id2word['e']]
print('e vector', e)
// e vector[0, 0, 1, 1, 0]
let simde = cosSimilarity(nj.array(d), nj.array(e));
print('similarity between d to e: ' + Math.floor(simde.get(0) * 100) + '%');
// similarity between d to e: 49%

これぐらい少ない語彙なら、共起行列を見ればある程度直感的にどの単語が似ているか判断できます。

With such a small vocabulary, co-occurrence matrices make it some what intuitive to determine which words are similar.

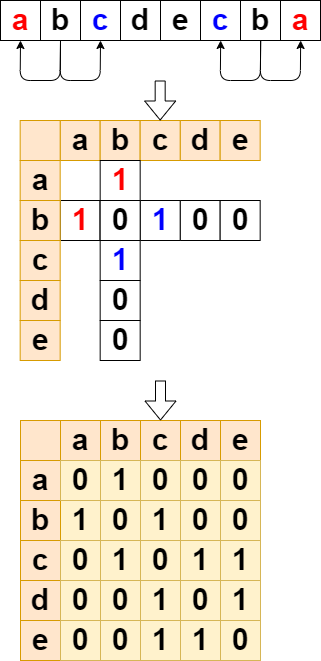
dとeはベクトルのパターンが似ていますね。もちろん同じパターンのベクトルなら類似度はほぼ100%になります。

"d" and "e" have similar vector pattern. Of course, vectors of the same pattern have almost 100% similarity.

See You Next Page!

p5.jsとnumjs - コサイン類似度 p5.js and numjs - Cosine Similarity