【Python】numpyの簡単な使い方と簡易的なニューラルネットワークの単純な構築方法
【Python】A simple way to use numpy and a simple way to build a neural network

YouTubeにアップした動画、「【Python】numpyの簡単な使い方と簡易的なニューラルネットワークの単純な構築方法」の補足説明の記事です。

Here's a little more about the 「【Python】A simple way to use numpy and a simple way to build a neural network」 video I uploaded to YouTube.

今回の動画は「機械学習」や「深層学習」において必要となる行列計算等の数学を使った計算を楽にしてくれる便利なモジュールであるnumpyを使用して、

ものすごく単純なニューラルネットワークを構築してみるところまでをアニメーションを使用して紹介しています。

前半部分がnumpyを使った基本的な行列計算方法、後半がニューラルネットワークの構築方法の説明です。

This video shows you how to build a simple neural network using a handy module called numpy,

which makes it easy to do the math calculations needed for "machine learning" and "deep learning".

The first half describes the basic matrix calculation method using numpy, and the second half describes how to build a neural network.

無駄な説明を省いて、忙しい時でも短時間で理解できるような動画です。

It's a video that can be understood in a short period of time even when you're busy, without any unnecessary explanation.

まずはpipを使ってnumpyをインストールします。

First we use pip to install numpy.

pip install numpy

次に簡単にnumpyの結果を試していくためにpythonのインタラクティブコンソールを立ち上げます。

Next, we'll launch the python interactive console to easily try out the results of numpy.

The shorter the name, the easier it is to type, so use [as] (Abbreviation of alias) to call numpy with the np.

import numpy as np

さっそくnumpyを試してみます。

we will try numpy immediately.

x = np.array([1,2,3])

まずnumpyの配列(ndarray)を作成します。

First, we create an array of numpy (ndarray).

x.shape

これは配列（ベクトル）の各次元のサイズを返します。

[shape] returns the size of each dimension in the numpy array.

行か列のベクトルなら(a,)のような形, 行列なら(a,b)のような形, 三次元なら(a,b,c)のような形になります。

A vector of rows and columns looks like (a,), a matrix looks like (a, b), and a three-dimensional looks like (a, b, c).

x.ndim

これはnumpyの配列(ndarray)の次元数を返します。

[ndim] returns the number of dimensions in the array (ndarray) of numpy.

四則計算:Four arithmetic operations

次に、numpy配列 (ndarray) に四則計算を使う方法を説明します。

The following shows how to use four arithmetic operations on the numpy array (ndarray).

行列同士の四則演算のやり方はとてもシンプルで、行列の各要素に別の行列の各要素を1対1で計算をしていくだけです。

The method of arithmetic operations between matrices is very simple, each element of a matrix is computed on a one-to-one basis with each element of another matrix.

>>> a=np.array([[1,2,3],[1,2,3]])
>>> a*np.array([[1,2],[1,2]])
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,3) (2,2)
>>> a*np.array([[1,2],[1,2,3]])
<stdin>:1: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,3) (2,)
>>> a*np.array([[1,2,3],[1,2,3],[])
  File "<stdin>", line 1
    a*np.array([[1,2,3],[1,2,3],[])
                                  ^
SyntaxError: closing parenthesis ')' does not match opening parenthesis '['
>>> a*np.array([[1,2,3],[1,2,3],[1,2,3]])
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,3) (3,3)

このようにエラーになるので各次元毎のサイズは合わせてください。

基本的には普通に足し算や割り算を行うだけです。

This is an error, so adjust the size for each dimension.

Basically, you just add and divide normally.

a=np.array([[1,2,3],[1,2,3]])
b=np.array([[1,2,3],[1,2,3]])

>>> a+b
array([[2, 4, 6],
       [2, 4, 6]])
>>> a-b
array([[0, 0, 0],
       [0, 0, 0]])
>>> a*b
array([[1, 4, 9],
       [1, 4, 9]])
>>> a/b
array([[1., 1., 1.],
       [1., 1., 1.]])

行列の細かい計算過程は動画を参照してください。

Please see the video for the detailed calculation process of the matrix.

続いてスカラー（一つの実数のこと）と行列の計算で使われているブロードキャストについての説明です。

説明は単純で、単一の実数であるスカラーを行列同士の計算として扱えるように、掛け合わせる対象のN×Nの行列に合わせて、numpyが自動でそのスカラーをN×Nの行列に複製してくれる機能です。

Next, let's look at the broadcast of numpy. It is used in scalar (a single real number) and matrix calculations. The broadcast is simple in that it automatically duplicates the scalar into an N×N matrix so that the scalar can be treated as a computation between matrices.

>>> np.array([[[1,2],[1,2]],[[1,2],[1,2]]])*2
array([[[2, 4],
        [2, 4]],

       [[2, 4],
        [2, 4]]])

ニューラルネットワークについての説明は自分の過去記事を読んでください。ここでは簡潔に述べます。

For an explanation of neural networks, read my previous blog post. So I'll keep it brief.

すごくシンプルなニューラルネットワークは入力する値と出力する値があるだけです。

A very simple neural network has only input and output values.

しかし単に入力された値を出力しているだけのネットワークだと、物事を「学習」させることができません。

However, if the network simply outputs the input value, it cannot be learned.

そこでネットワークの層を増やし、関数として扱えるようにした後、出力された値と正解となるデータを照らし合わせます。

So we increase the layer of the network so that it can be treated as a function, and then we compare the output with the correct data.

関数として扱えることの最大のメリットは変数を変化させることによって、出力値と正解値との間の誤差に対して調整を行えるからです。

The biggest advantage of being treated as a function is that you can adjust the error between the output value and the correct value by changing the variable.

とどのつまり、ニューラルネットワークとは単なる関数です。ある入力に対して、何らかの計算を行い出力を返します。その計算方法が分かっていれば、変数を調整して、望ましい答えに近づけることができます。

After all, neural networks are just functions. Performs some computation on an input and returns the output. If you know how to calculate it, you can adjust the variables to approximate the desired answer.

その変数となる値が重みとバイアスです。

The variables are weight and bias.

重みは日本語にすると大変分かりにくいので、言い換えると、「入力された値がどれだけ重要か調整する値」と思ってください。

The weight is very hard to understand in Japanese, so in other words, think "The value to adjust how important the entered value is".

バイアスも日本語での理解が難しいです。一次関数のグラフで例えると、「切片」なります。このバイアスがあると例え入力値と重みがゼロでも何かしらの数値が一定数出力層に与えられます。

Bias is also difficult to understand in Japanese. In a graph of a linear function, this would be "Intercept". With this bias, even if the input value or weight are zero, some number is given to the constant output layer.

物事の偏った考えで用いられるバイアスと同じです。人はこのバイアスがあることによって正しく物事を見れないことが多々あります。

It's the same bias we use in biased thinking. This bias often prevents people from seeing things correctly.

なんでこんなことをするかというと、ニューラルネットワークは人間の脳のネットワークを模したものだからです。人は学習する時に常にこのバイアスが掛かっている状態と仮定して、学習過程においてこのバイアスは必要であろうと考えたからです。 つまり人はバイアスがある状態で学習して、最初に必ず間違えると過程し、そこでその間違いに気付いてそのバイアスを調整することによって学習を進めるのだろうといった具合に。 つまりニューラルネットワークはまず最初に間違えさせてから、その間違えを修正することによって学習を進めるように設計されています。

The reason for doing this is because neural networks mimic networks in the human brain. We assumed that this bias was always present when learning, and we thought that this bias would be necessary in the learning process. In other words, people learn with a bias, and when they make a mistake at first, they process it, and then they notice the mistake and adjust the bias to get better at learning. In other words, neural networks are designed to let you make mistakes first, and then learn by correcting those mistakes.

行列の積

話が大分長くなってしまったので最後に行列の積の説明で終わりです。

It's a long story, so I'll end with the explanation of the matrix product.

この行列の積は今までの行列同士の演算方法と少し様子が違います。

This matrix product is a little different from the four arithmetic operations of calculating matrices described above.

例えば、2行3列の行列があります。この時掛ける方の行列の行は3行と掛けられる行列の3列と数が一致しなければなりません。つまり２x３ に対して　３xNの行列を用意しなくてはなりません。

For example, a matrix with two rows and three columns. The row of the matrix to be multiplied must match column of the matrix to be multiplied. That is, there must be a 2×3 matrix for a 2×N matrix.

実際の計算方法は動画を見ていただきたいのですが、なぜこんな計算をするのか、その意味を考えていきます。

I want you to watch the video for the actual calculation method, but I will consider the meaning of this calculation.

結論からいうと、大量の計算を楽に速く行うためです。

The bottom line is that you can do a lot of calculations easily and quickly.

そもそもコンピュータは「並列計算」が得意です。

In the first place, computers are good at "parallel computing".

行列はこの「並列計算」を可能にします。

The matrix makes this "parallel computing" possible.

例を見せます。まず普通のFor文を使った「一つずつ計算をする方法」とnumpyによる線形代数を使った「並列処理による一括計算」を見てみましょう。

Let me show you an example. Let's first look at "way of doing one calculation at a time" using the regular For statement and "Bulk Calculations with Parallel Processing" using linear algebra by numpy.

# Calculations that do not use numpy
x = [[1,2],[3,4],[5,6]] # three rows, two colmuns
y = [[1,2,3],[4,5,6]] # two rows, three colmuns
a = []
for i in range(len(x)):
    accum = []
    for j in range(len(y[0])):
        elem = 0
        for k in range(len(y)): 
            elem += x[i][k] * y[k][j]
        accum.append(elem)
    a.append(accum)
print(a)
[[9, 12, 15], [19, 26, 33], [29, 40, 51]]

# Using Linear Algebra with numpy
X = np.array([[1,2],[3,4],[5,6]])
Y = np.array([[1,2,3],[4,5,6]])
A = np.dot(X,Y)
print(A)
array([[ 9, 12, 15],
       [19, 26, 33],
       [29, 40, 51]])

コードの量が少なくなってスッキリしました。さらにここで注目するのはnumpyでの処理は行列を一つの塊として計算していることです。 それはコードを見れば直観的に理解できます。コンピューターに並列処理をさせるようにする為に行列の仕組みが必要なのです。 深層学習等ではそれこそ万を越える配列を処理します。 それを全てFor文で一つずつ計算するとなると、いくら人間の数百倍計算速度が高いCPUでもどれだけ大変な作業と時間がかかるか想像できるでしょう。

The amount of cords has been reduced, so it's clean. What's more, it's important to note here that the process in numpy is to compute the matrix as a whole. You can understand it intuitively by looking at the code. We need a matrix mechanism to get computers to do parallel processing. In deep learning and so on, that's dealing with tens of thousands of arrays. You can imagine how much work and time it would take to compute all of them in For statements, even on CPUs that are hundreds of times faster than humans.

numpyはC/C++で書かれていて、ndarrayはメモリの連続領域上に確保されるようになっています。 またnumpyにはndarrayの全要素に対して演算処理を行うユニバーサル関数と言われるものが備わっています。 これらのおかげで前述の通り、高速な並列計算処理の恩恵を受けて、深層学習に際に必要な膨大な計算量が可能になるわけです。

Numpy is written in C/C + +, and ndarray is reserved on a contiguous block of memory. Numpy also has a universal function that performs operations on all elements of ndarray. As mentioned earlier, this allows the enormous amount of computation required for deep learning to benefit from fast parallel computing.

ここで行列の積の計算方法を思い出してください。

Now remember how to calculate the matrix product.

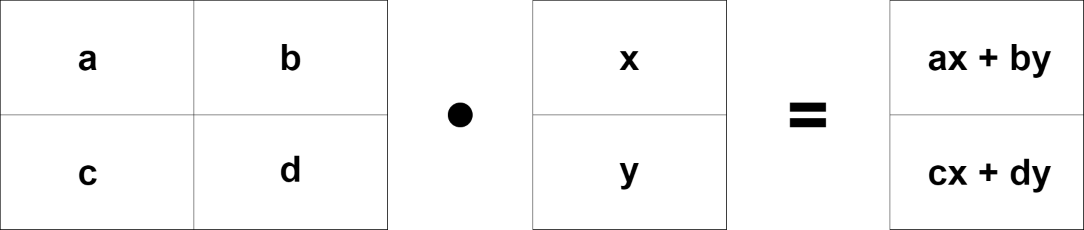
では少しだけ視点を変えて右側のベクトルが上から入り、右に行列の結果が表れるように入れ替えてみましょう。

Let's change the point of view a little bit so that the vector on the right goes in from the top and the result of the matrix appears on the right.

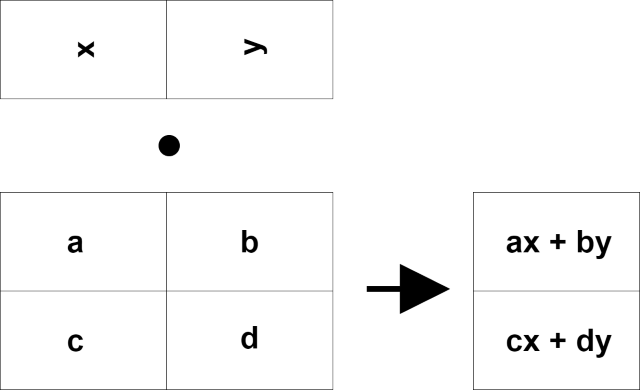
何か一気に計算ができそうな気がしませんか？

Don't you think you can do some calculation at once?

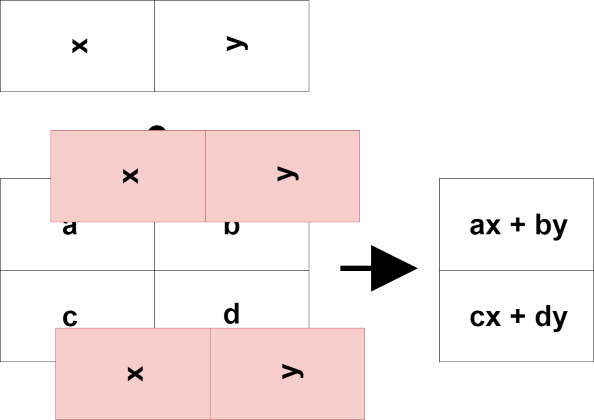
一つ一つ計算する場合と比べてどうでしょうか？

How does it compare to calculating one by one?

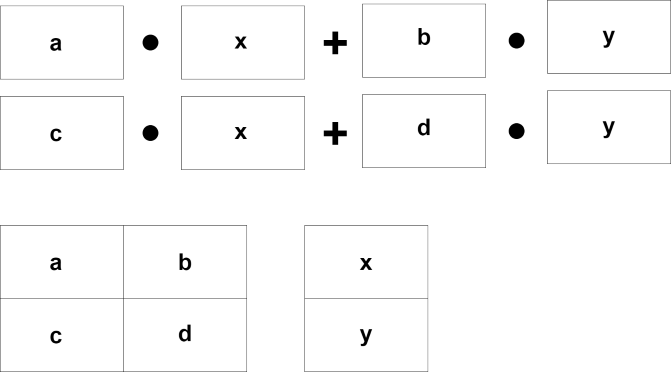
因みに、あくまで物の例えですが、もし並べられたコンピューターメモリ上にある数値が散乱していて、あっちにいったりこっちにいったりしていたとします。

By the way, it's just a metaphor for things. Imagine if the numbers in the array of computer memory were scattered around, going in and out.

こんな感じで綺麗にある数値が綺麗に並べられて、綺麗に流れるように計算、もしくは一度にいっぺんに計算できたとしたら？さきほどと比べてどうなるでしょうか？

What if you were able to calculate a number in such a way that it is neatly arranged and flows smoothly, or at the same time? How is it compared to the previous time?

あくまで物の例えです。しかし、見れば見るほどメモリを上手く使った計算と行列の考えや計算方法とは似ていますね。

It's just a metaphor. However, the more you look at it, the more it resembles the idea and calculation method of the matrix and the calculation using memory well.

以上です。お疲れ様です。

See You Next Page!