Processingを数学のノート代わりに使う - Part 1
Use Processing as a math notebook - Part 1

今回はYouTubeにアップした動画、「Use Processing as a math note」の補足説明の記事です。

Here's a little more about the "Use Processing as a math note" video I uploaded to YouTube.

全体の説明は動画に任せるとして、説明が必要だろうと思われる関数やアルゴリズム等を時系列順に紹介していきMASU。

I'll leave the entire explanation to the video, but I'll show you the functions, algorithms, and so on, in chronological order.

y座標とsinθの関係性を図で示します。

The following illustration shows the relationship between the y coordinate and sinθ.

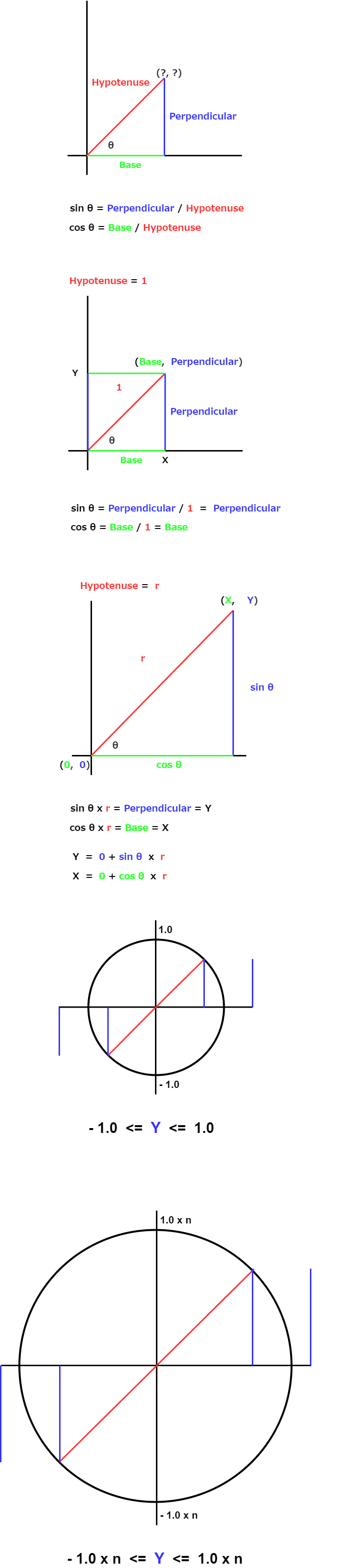
X軸とY軸の座標系でcosθ、sinθを考えると、 cosθはX座標と、X軸とY軸が作る三角形の斜辺との対比です。 sinθはY座標と、X軸とY軸が作る三角形の斜辺との対比です。 ここで斜辺を1とすると、cosθはX座標、sinθはY座標になります。 このθ、つまり角度は斜辺が長くなっても変わらないので、 （この傾きはXとYの対比で求められるので、XとYの比率が変わらなければ傾きは変わりません） （Y ＊ r / X ＊ r ：：： X = 2、Y ＝ ４、 r ＝ １、２、３ … ：：： ２/４ ＝ 0.5 ： ４/８ ＝ 0.5 ： ８/１６ ＝ 0.5 ： …） 角度と斜辺の長ささえ決めてしまえば、X座標とY座標が求められます。

If you consider cosθ and sinθ in the coordinate systems of the X and Y axes, cosθ is the contrast between the X coordinate and the Hypotenuse of the triangle formed by the X and Y axes. sinθ is the contrast between the Y coordinate and the Hypotenuse of the triangle formed by the X and Y axes. If the Hypotenuse is 1, cosθ is the X coordinate and sinθ is the Y coordinate. This θ, that is, the angle does not change even if the Hypotenuse becomes longer. (Because this slope is determined by the contrast between X and Y, the slope does not change unless the ratio between X and Y changes.) （Y ＊ r / X ＊ r ：：： X = 2、Y ＝ ４、 r ＝ １、２、３ … ：：： ２/４ ＝ 0.5 ： ４/８ ＝ 0.5 ： ８/１６ ＝ 0.5 ： …） Once the angle and the length of the Hypotenuse are determined, the X and Y coordinates are determined.

vertex（x、y）は画面上の指定した座標（x、y）に点を作ります。

vertex(x,y) creates a point at the specified coordinates (x,y) on the screen.

そしてbeginShape（）とendShape（）で囲めば、Vertex（x、y）同士が線で繋がれて、色々な図形が表現できます。

And if you enclose with beginShape() and endShape(), vertex(x,y) is connected with each other by a line, and various figures can be expressed.

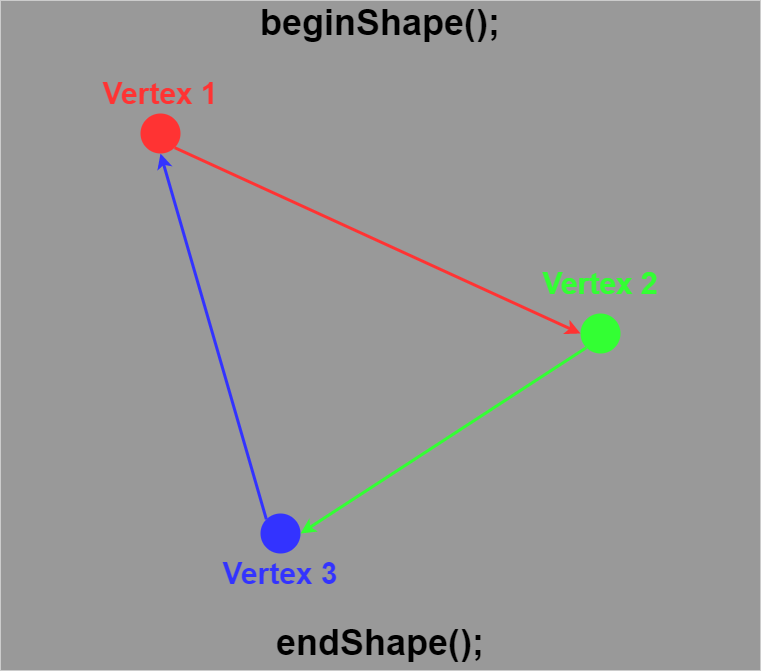
Processingを使ってインタラクティブに理解するために以下のコードを実行してみてください。

To understand it intuitively using Processing, please check it by executing the following code.

void setup(){
  size(640,360);
}

void draw(){
  background(255);
  
  textSize(21);
  
  fill(0);
  beginShape();
  vertex(300,100);
  vertex(400,200);
  vertex(mouseX,200);
  vertex(mouseX,mouseY);
  endShape();
  
  fill(255,0,0);
  text("vertex1",310,90);
  ellipse(300,100, 10,10);
  fill(0,255,0);
  text("vertex2",410,190);
  ellipse(400,200, 10, 10);
  fill(0,0,255);
  text("vertex3",mouseX,220);
  ellipse(mouseX,200, 10, 10);
  fill(255,0,255);
  text("vertex4",mouseX,mouseY);
  ellipse(mouseX,mouseY, 10, 10);
}

Map関数を簡単に説明すると、数値の幅の変換器です。

The map function is simply a numeric width converter.

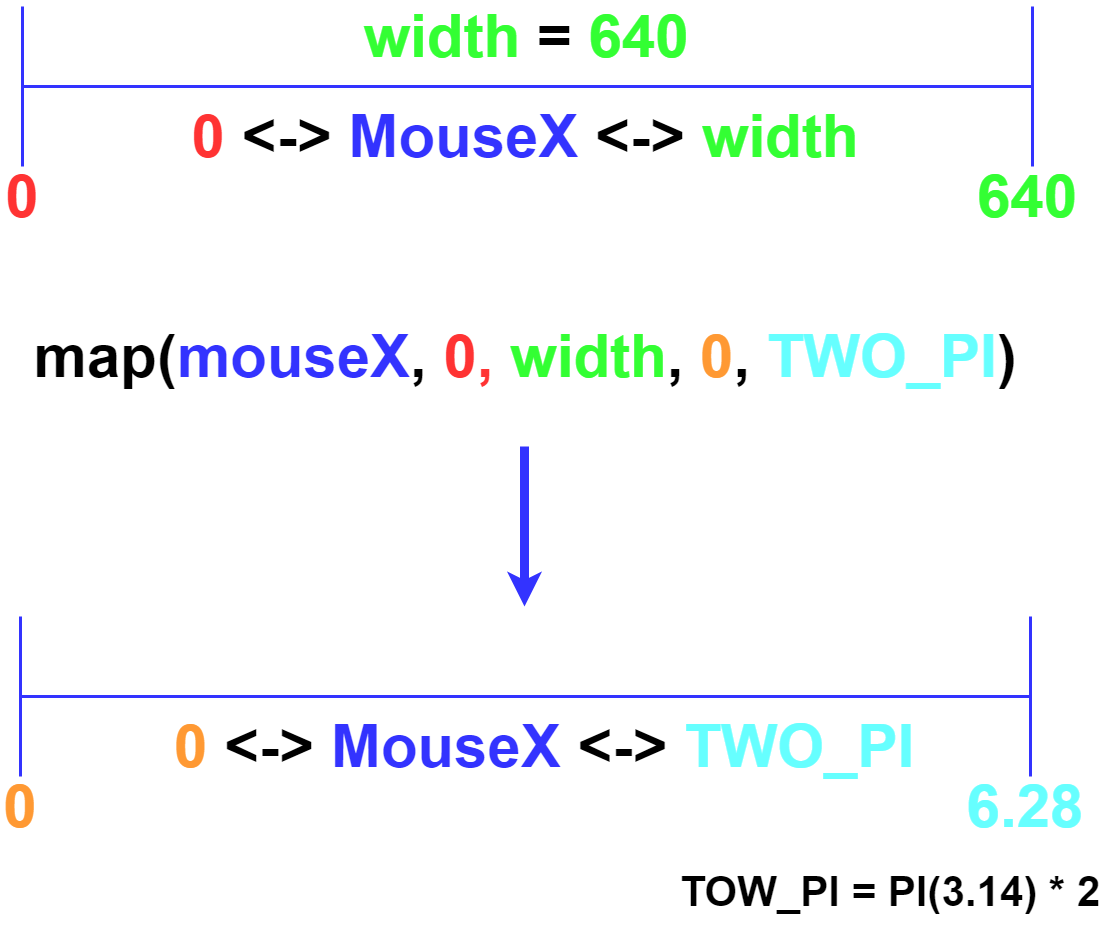
例えば、Size関数で画面の横幅を640、縦幅を360に設定したとします。 すると、横幅は０から640までの数値の幅があります。 Map関数を使えば、この０から６４０までの数値の幅を自由に設定することができます。

For example, suppose you use Size function to set the screen width to 640 and height to 360. The width can then be determined by a number between 0 and 640. You can use the Map function to set the width of this number to the width of another number.

たとえば半径が１の円を動くSinθの値は−１から１まであります。 横幅の０から６４０までを0からTWO_PIまでの数値幅に変換すると、 マウスの動きでSinθの動きを表現できるようになります。

For example, the value of Sinθ in a circle with a radius of 1 ranges from -1 to 1. When the width from 0 to 640 is converted to the numerical width from 0 to TOW_PI, The movement of the mouse can represent the movement of Sinθ.

void setup(){
  size(640,360);
}

void draw(){
  background(255);
  
  float r = 1 * 300;
  
  float angle = map(mouseX, 0, width, 0, TWO_PI);
  
  noFill();
  strokeWeight(1);
  stroke(0);
  ellipse(width/2, height/2, r, r);
  
  float x = width/2 + cos(angle) * r/2;
  float y = height/2 + sin(angle) * r/2;
  
  strokeWeight(3);
  stroke(255, 0,0);
  line(width/2, height/2, x, y);
  
  fill(0);
  textSize(21);
  
  if (mouseX > width/2) {
    textAlign(RIGHT);
  } else {
    textAlign(LEFT);
  }
  text("mouseX: " + mouseX, mouseX, mouseY);
  text("convert to radians: " + angle, mouseX, mouseY+30);
}

長くなってしまったのでPart２へ続きます。

Since the blog post is long, I will divide it into two parts.